【题目】平行四边形ABCD两邻边的长m,n是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)求k的取值范围.
(2)当k为何值时,四边形ABCD的两条对角线的长相等,且都等于![]() ,求出这时四边形ABCD的周长和面积.
,求出这时四边形ABCD的周长和面积.
参考答案:
【答案】(1)k的取值范围是k>![]() ;(2)四边形ABCD的周长是4,面积是
;(2)四边形ABCD的周长是4,面积是![]() .
.
【解析】
(1)根据题意求出△=b2-4ac=(-k)2-4×1×(![]() )≥0,m+n=k>0,mn=
)≥0,m+n=k>0,mn=![]() >0,求出不等式组的解集即可;
>0,求出不等式组的解集即可;
(2)得出四边形是矩形,根据勾股定理和根与系数的关系求出k,求出方程的解,即可求出矩形的周长和面积.
(1)∵平行四边形ABCD的两邻边的长m,n是关于x的方程x2kx+![]() =0的两个实数根,
=0的两个实数根,
∴△=b2-4ac=(-k)2-4×1×(![]() )≥0,m+n=k>0,mn=
)≥0,m+n=k>0,mn=![]() >0,
>0,
(k-1)2≥0,k>0,k>![]() ,
,
即k的取值范围是k>![]() ;
;
(2)∵四边形是平行四边形,且四边形的对角线相等,
∴四边形ABCD是矩形,
∴∠ABC=90°,
由勾股定理得:m2+n2=(![]() )2,
)2,
即(m+n)2-2mn=![]() ,
,
∵m+n=k,mn=![]() ,
,
∴k2-2(![]() )=
)=![]() ,
,
k1=2,k2=-1(因为由(1)得出k>![]() ,所以此时的值舍去),
,所以此时的值舍去),
把k=2代入方程得:x2-2x+![]() =0,
=0,
解方程得:m=![]() ,n=
,n=![]() 或n=
或n=![]() ,m=
,m=![]() ,
,
∴矩形ABCD的周长是2×(![]() +
+![]() )=4,面积是
)=4,面积是![]() ×
×![]() =
=![]() .
.
即此时四边形ABCD的周长是4,面积是![]() .
.
-
科目: 来源: 题型:
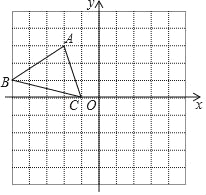
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣2,3),B(﹣5,1),C(﹣1,0).
(1)在图中作出△ABC关于x轴的对称图形△A1B1C1;
(2)在图中作出△ABC关于原点O成中心对称的图形△A2B2C2,并写出A2点的坐标;
(3)在y轴上找一点P,使△PAC的周长最小,请直接写出点P的坐标.
-
科目: 来源: 题型:
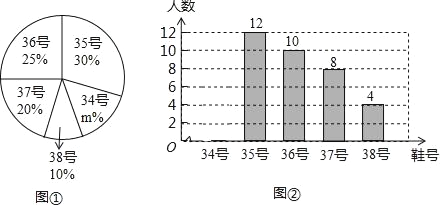
查看答案和解析>>【题目】为了方便学生参加体育锻炼,某学校准备购买一批运动鞋供学生体育锻炼借用.现从各年级随机抽取了部分学生的鞋号,绘制出如下不完整的统计图①和图②,请根据有关信息,解答下列问题:
(1)填空:本次随机抽样调查的学生为 名,本次调查获取的样本数据的中位数是 号,众数是 号;
(2)补全条形统计图;
(3)根据样本数据,若学校计划购买800双运动鞋,建议购买34号运动鞋多少双?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件.
(1)求商场经营该商品原来一天可获利润多少元?
(2)设后来该商品每件降价x元,,商场一天可获利润y元.
①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?
②求出y与x之间的函数关系式,结合题意写出当x取何值时,商场获利润不少于2160元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD与四边形CEFG是两个正方形,边长分别为a,b,其中B,C,E在一条直线上,G在线段CD上,三角形AGE的面积为S.
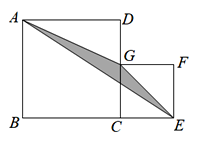
(1)①当a=5,b=3时,求S的值;
②当a=7,b=3时,求S的值;
(2)从以上结果中,请你猜想S与a,b中的哪个量有关?用字母a,b表示S,并对你的猜想进行证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.
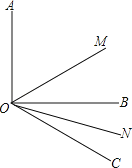
(1)求∠MON的度数;
(2)如果∠AOB=α,其他条件不变,求∠MON的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区为了美化环境,计划分两次购进A,B两种花,第一次分别购进A,B两种花30棵和15棵,共花费675元;第二次以同样的单价分别购进A、B两种花12棵和5棵,第二次花费265元.
(1)求A、B两种花的单价分别是多少元?
(2)若购买A、B两种花共31棵,且B种花的数量不多于A种花的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.
相关试题

