【题目】如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣![]() ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.

参考答案:
【答案】(1) A(﹣1,0),B(3,0);(2)存在,P(![]() );(3) m=﹣1或﹣
);(3) m=﹣1或﹣![]() .
.
【解析】试题分析:(1)将![]() 化为交点式,即可得到
化为交点式,即可得到![]() 两点的坐标;
两点的坐标;
(2)先用待定系数法得到抛物线C1的解析式,过点P作PQ∥y轴,交BC于Q,用待定系数法得到直线BC的解析式,再根据三角形的面积公式和配方法得到![]() 面积的最大值;
面积的最大值;
(3)先表示出![]() 再分两种情况:①
再分两种情况:①![]() 时;
时;
②![]() 时,讨论即可求得
时,讨论即可求得![]() 的值.
的值.
试题解析:(1)![]()
∵m≠0,
∴当y=0时,![]()
∴A(1,0),B(3,0);
(2)设![]() ,将A. B.C三点的坐标代入得:
,将A. B.C三点的坐标代入得:
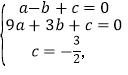 解得
解得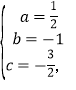
故![]()
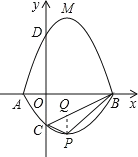
如图:过点P作PQ∥y轴,交BC于Q,
由B.C的坐标可得直线BC的解析式为:![]()
设![]() 则
则![]()
![]()
![]()
当![]() 时,
时,![]() 有最大值,
有最大值,![]()
![]()
![]()
(3)![]()
顶点M坐标(1,4m),
当x=0时,y=3m,
∴D(0,3m),B(3,0),
![]()
![]()
![]()
当△BDM为Rt△时有:![]() 或
或![]()
![]() 时有:
时有:![]()
解得m=1(∵m<0,∴m=1舍去);
![]() 时有:
时有:![]()
解得![]() (
(![]() 舍去).
舍去).
综上,m=1或![]() 时,
时,![]() 为直角三角形.
为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD与四边形CEFG是两个正方形,边长分别为a,b,其中B,C,E在一条直线上,G在线段CD上,三角形AGE的面积为S.
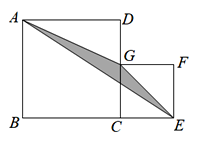
(1)①当a=5,b=3时,求S的值;
②当a=7,b=3时,求S的值;
(2)从以上结果中,请你猜想S与a,b中的哪个量有关?用字母a,b表示S,并对你的猜想进行证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.
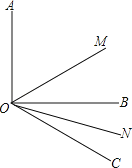
(1)求∠MON的度数;
(2)如果∠AOB=α,其他条件不变,求∠MON的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区为了美化环境,计划分两次购进A,B两种花,第一次分别购进A,B两种花30棵和15棵,共花费675元;第二次以同样的单价分别购进A、B两种花12棵和5棵,第二次花费265元.
(1)求A、B两种花的单价分别是多少元?
(2)若购买A、B两种花共31棵,且B种花的数量不多于A种花的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知RtΔABC,∠C=90°,D为BC的中点.以AC为直径的圆O交AB于点E.
(1)求证:DE是圆O的切线.
(2)若AE:EB=1:2,BC=6,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积在数量上相等,则这个点叫做和谐点.
(1)判断点M(﹣1,2),N(﹣4,﹣4)是否为和谐点,并说明理由;
(2)若和谐点P(a,3)在直线y=﹣x+b(b为常数)上,试求a,b的值.
-
科目: 来源: 题型:
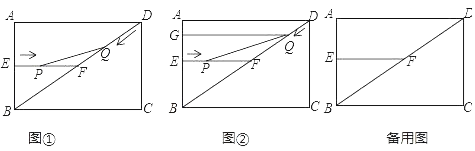
查看答案和解析>>【题目】如图1,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是AB、BD的中点,连接EF,点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时,点Q从点D出发,沿DB方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s,解答下列问题:
(1)求证:△BEF∽△DCB;
(2)当点Q在线段DF上运动时,若△PQF的面积为0.6cm2,求t的值;
(3)如图2过点Q作QG⊥AB,垂足为G,当t为何值时,四边形EPQG为矩形,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?试说明理由.
相关试题

