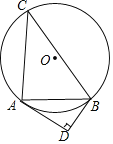
【题目】如图,已知⊙O的半径为5,△ABC是⊙O的内接三角形,AB=8,.过点B作⊙O的切线BD,过点A作AD⊥BD,垂足为D.
(1)求证:∠BAD+∠C=90°
(2)求线段AD的长.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由弦切角等于同弧所对的圆周角得:∠C=∠ABD,再根据直角三角形两锐角互余得出结论;
(2)作弦心距,由勾股定理得:OE=3,再证明△OEB∽△BDA,列比例式可以求AD的长.
:(1)∵BD为⊙O的切线,
∴∠C=∠ABD,
∵AD⊥BD,
∴∠ADB=90°,
∴∠BAD+∠ABD=90°,
∴∠C+∠BAD=90°,
(2)连接OB,过O作OE⊥AB于E,
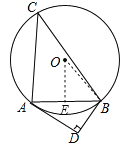
∴AE=BE=![]() AB=4,
AB=4,
由勾股定理得:OE=![]() =
=![]() =3,
=3,
∵BD为⊙O的切线,
∴OB⊥BD,
∴∠OBD=90°,
∵∠ADB=90°,
∴AD∥OB,
∴∠DAB=∠ABO,
∵∠D=∠OEB=90°,
∴△OEB∽△BDA,
∴![]() ,
,
∴![]() ,
,
∴AD=![]() ;
;
则线段AD的长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了创建绿色生态城市,在城东建了“东州湖”景区,小明和小亮想测量“东州湖”东西两端A、B间的距离.于是,他们去了湖边,如图,在湖的南岸的水平地面上,选取了可直接到达点B的一点C,并测得BC=350米,点A位于点C的北偏西73°方向,点B位于点C的北偏东45°方向.请你根据以上提供的信息,计算“东州湖”东西两端之间AB的长.(结果精确到1米)(参考数据:sin73°≈0.9563,cos73≈0.2924,tan73°≈3.2709,
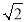 ≈1.414.)
≈1.414.)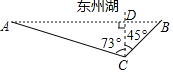
-
科目: 来源: 题型:
查看答案和解析>>【题目】上周六上午
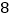 点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离
点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离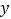 (千米)与他们路途所用的时间
(千米)与他们路途所用的时间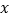 (时)之间的函数图象,请根据以上信息,解答下列问题:
(时)之间的函数图象,请根据以上信息,解答下列问题:(1)求直线
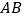 所对应的函数关系式;
所对应的函数关系式;(2)已知小颖一家出服务区后,行驶
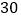 分钟时,距姥姥家还有
分钟时,距姥姥家还有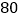 千米,问小颖一家当天几点到达姥姥家?
千米,问小颖一家当天几点到达姥姥家?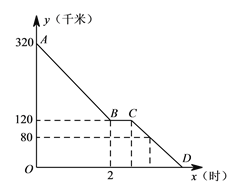
-
科目: 来源: 题型:
查看答案和解析>>【题目】孙老师在上《等可能事件的概率》这节课时,给同学们提出了一个问题:“如果同时随机投掷两枚质地均匀的骰子,它们朝上一面的点数和是多少的可能性最大?”同学们展开讨论,各抒己见,其中小芳和小超两位同学给出了两种不同的回答.小芳认为6的可能性最大,小超认为7的可能性最大.你认为他们俩的回答正确吗?请用列表或画树状图等方法加以说明.(骰子:六个面上分别刻有1,2,3,4,5,6个小圆点的小正方体.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,△AOB是等腰直角三角形,∠AOB=90°,点A(2,1).
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的函数表达式;
(3)在(2)所求的抛物线上,是否存在一点P,使四边形ABOP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
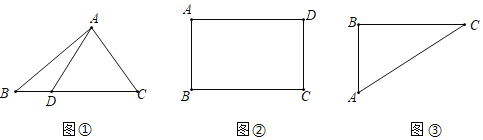
查看答案和解析>>【题目】问题提出(1)如图①,在△ABC中,BC=6,D为BC上一点,AD=4,则△ABC面积的最大值是 .
问题探究(2)如图②,已知矩形ABCD的周长为12,求矩形ABCD面积的最大值.
问题解决(3)如图③,△ABC是葛叔叔家的菜地示意图,其中AB=30米,BC=40米,AC=50米,现在他想利用周边地的情况,把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地,用来建鱼塘.已知葛叔叔欲建的鱼塘是四边形ABCD,且满足∠ADC=60°.你认为葛叔叔的想法能否实现?若能,求出这个四边形鱼塘周长的最大值;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
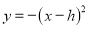 (
(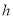 为常数),当自变量
为常数),当自变量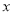 的值满足
的值满足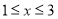 时,其对应的函数值
时,其对应的函数值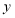 的最大值为
的最大值为 ,则
,则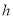 的值为 ( )
的值为 ( )A.2或4B.0或-4C.2或-4D.0或4
相关试题

