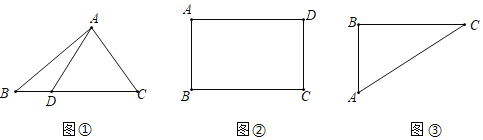
【题目】问题提出(1)如图①,在△ABC中,BC=6,D为BC上一点,AD=4,则△ABC面积的最大值是 .
问题探究(2)如图②,已知矩形ABCD的周长为12,求矩形ABCD面积的最大值.
问题解决(3)如图③,△ABC是葛叔叔家的菜地示意图,其中AB=30米,BC=40米,AC=50米,现在他想利用周边地的情况,把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地,用来建鱼塘.已知葛叔叔欲建的鱼塘是四边形ABCD,且满足∠ADC=60°.你认为葛叔叔的想法能否实现?若能,求出这个四边形鱼塘周长的最大值;若不能,请说明理由.
参考答案:
【答案】(1)12;(2)9;(3)能实现;170(米).
【解析】
(1)当AD⊥BC时,△ABC的面积最大.
(2)由题意矩形邻边之和为6,设矩形的一边为m,另一边为6﹣m,可得S=m(6﹣m)=﹣(m﹣3)2+9,利用二次函数的性质解决问题即可.
(3)由题意,AC=100,∠ADC=60°,即点D在优弧ADC上运动,当点D运动到优弧ADC的中点时,四边形鱼塘面积和周长达到最大值,此时△ACD为等边三角形,计算出△ADC的面积和AD的长即可得出这个四边形鱼塘面积和周长的最大值.
(1)如图①中,
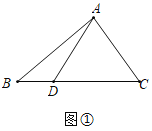
∵BC=6,AD=4,
∴当AD⊥BC时,△ABC的面积最大,最大值=![]() ×6×4=12.
×6×4=12.
故答案为12.
(2)∵矩形的周长为12,
∴邻边之和为6,设矩形的一边为m,另一边为6﹣m,
∴S=m(6﹣m)=﹣(m﹣3)2+9,
∵﹣1<0,
∴m=3时,S有最大值,最大值为9.
(3)如图③中,
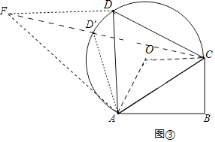
∵AC=50米,AB=40米,BC=30米,
∴AC2=AB2+BC2
∴∠ABC=90°,
作△AOC,使得∠AOC=120°,OA=OC,以O为圆心,OA长为半径画⊙O,
∵∠ADC=60°,
∴点D在优弧ADC上运动,
当点D是优弧ADC的中点时,四边形ABCD面积取得最大值,
设D′是优弧ADC上任意一点,连接AD′,CD′,延长CD′到F,使得D′F=D′A,连接AF,则∠AFC=30°=![]() ∠ADC,
∠ADC,
∴点F在D为圆心DA为半径的圆上,
∴DF=DA,
∵DF+DC≥CF,
∴DA+DC≥D′A+D′C,
∴DA+DC+AC≥D′A+D′C+AC,
∴此时四边形ADCB的周长最大,最大值=40+30+50+50=170(米).
答:这个四边形鱼塘周长的最大值为170(米).
-
科目: 来源: 题型:
查看答案和解析>>【题目】孙老师在上《等可能事件的概率》这节课时,给同学们提出了一个问题:“如果同时随机投掷两枚质地均匀的骰子,它们朝上一面的点数和是多少的可能性最大?”同学们展开讨论,各抒己见,其中小芳和小超两位同学给出了两种不同的回答.小芳认为6的可能性最大,小超认为7的可能性最大.你认为他们俩的回答正确吗?请用列表或画树状图等方法加以说明.(骰子:六个面上分别刻有1,2,3,4,5,6个小圆点的小正方体.)
-
科目: 来源: 题型:
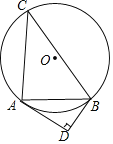
查看答案和解析>>【题目】如图,已知⊙O的半径为5,△ABC是⊙O的内接三角形,AB=8,.过点B作⊙O的切线BD,过点A作AD⊥BD,垂足为D.
(1)求证:∠BAD+∠C=90°
(2)求线段AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,△AOB是等腰直角三角形,∠AOB=90°,点A(2,1).
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的函数表达式;
(3)在(2)所求的抛物线上,是否存在一点P,使四边形ABOP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
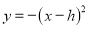 (
(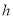 为常数),当自变量
为常数),当自变量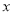 的值满足
的值满足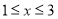 时,其对应的函数值
时,其对应的函数值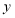 的最大值为
的最大值为 ,则
,则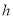 的值为 ( )
的值为 ( )A.2或4B.0或-4C.2或-4D.0或4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
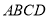 中,
中,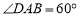 ,
,  , 点
, 点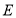 在边
在边 上,且
上,且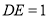 ,点
,点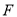 为线段
为线段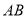 上一动点(不与点
上一动点(不与点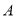 重合),将菱形沿直线
重合),将菱形沿直线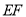 折叠,点
折叠,点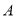 的对应点为点
的对应点为点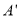 ,当
,当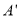 落在菱形的对角线上时,
落在菱形的对角线上时,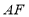 的长为__________.
的长为__________.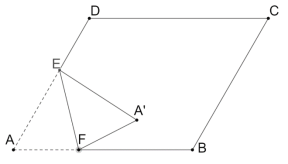
-
科目: 来源: 题型:
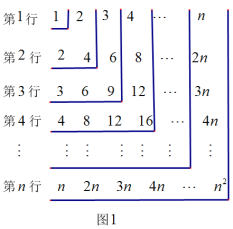
查看答案和解析>>【题目】如图1,观察数表,如何计算数表中所有数的和?
方法1:如图1,先求每行数的和:
第1行
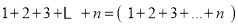
第2行
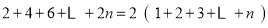
第n行
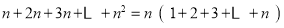
故表中所有数的和:
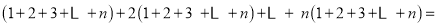 ;
;
方法2:如图2.依次以第1行每个数为起点,按顺时针方向计算各数的和:
第1组
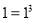
第2组
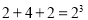
第3组
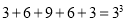
…
第
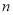 组
组 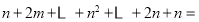 ,
,用这
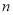 组数计算的结果,表示数表中所有数的和为: ,
组数计算的结果,表示数表中所有数的和为: ,综合上面两种方法所得的结果可得等式: ;
利用上面得到的规律计算:
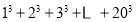 .
.
相关试题

