【题目】(模型建立)
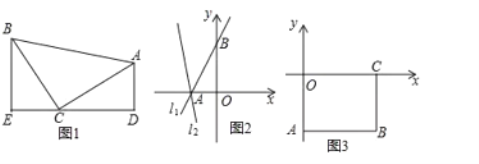
(1)如图1,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(模型应用)
(2)已知直线![]() :
:![]() 与坐标轴交于点
与坐标轴交于点![]() 、
、![]() ,将直线
,将直线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至直线
至直线![]() ,如图2,求直线
,如图2,求直线![]() 的函数表达式;
的函数表达式;
(3)如图3,长方形![]() ,
,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 、
、![]() 分别在坐标轴上,点
分别在坐标轴上,点![]() 是线段
是线段![]() 上的动点,点
上的动点,点![]() 是直线
是直线![]() 上的动点且在第四象限.若
上的动点且在第四象限.若![]() 是以点
是以点![]() 为直角顶点的等腰直角三角形,请直接写出点
为直角顶点的等腰直角三角形,请直接写出点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)见解析;(2)y=7x21;(3)D(4,2)或(![]() ,
,![]() ).
).
【解析】
(1)根据△ABC为等腰直角三角形,AD⊥ED,BE⊥ED,可判定![]() ;
;
(2)①过点B作BC⊥AB,交l2于C,过C作CD⊥y轴于D,根据△CBD≌△BAO,得出BD=AO=3,CD=OB=4,求得C(4,7),最后运用待定系数法求直线l2的函数表达式;
(3)根据△APD是以点D为直角顶点的等腰直角三角形,当点D是直线y=2x+6上的动点且在第四象限时,分两种情况:当点D在矩形AOCB的内部时,当点D在矩形AOCB的外部时,设D(x,2x+6),分别根据△ADE≌△DPF,得出AE=DF,据此列出方程进行求解即可.
解:(1)证明:∵△ABC为等腰直角三角形,
∴CB=CA,∠ACD+∠BCE=90°,
又∵AD⊥ED,BE⊥ED,
∴∠D=∠E=90°,∠EBC+∠BCE=90°,
∴∠ACD=∠EBC,
在△ACD与△CBE中,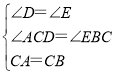 ,
,
∴![]() (AAS);
(AAS);
(2)①如图2,过点B作BC⊥AB,交l2于C,过C作CD⊥y轴于D,
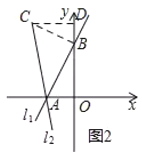
∵∠BAC=45°,
∴△ABC为等腰直角三角形,
由(1)可知:△CBD≌△BAO,
∴BD=AO,CD=OB,
∵直线l1:y=![]() x+4中,若y=0,则x=3;若x=0,则y=4,
x+4中,若y=0,则x=3;若x=0,则y=4,
∴A(3,0),B(0,4),
∴BD=AO=3,CD=OB=4,
∴OD=4+3=7,
∴C(4,7),
设l2的解析式为y=kx+b,则![]() ,
,
解得:![]() ,
,
∴l2的解析式为:y=7x21;
(3)D(4,2)或(![]() ,
,![]() ).
).
理由:当点D是直线y=2x+6上的动点且在第四象限时,分两种情况:
当点D在矩形AOCB的内部时,如图,过D作x轴的平行线EF,交直线OA于E,交BC于F,
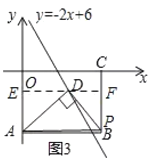
设D(x,2x+6),则OE=2x6,AE=6(2x6)=122x,DF=EFDE=8x,
由(1)可得,△ADE≌△DPF,则DF=AE,即:122x=8x,
解得x=4,
∴2x+6=2,
∴D(4,2),
此时,PF=ED=4,CP=6=CB,符合题意;
当点D在矩形AOCB的外部时,如图,过D作x轴的平行线EF,交直线OA于E,交直线BC于F,
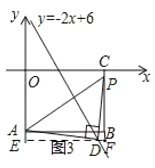
设D(x,2x+6),则OE=2x6,AE=OEOA=2x66=2x12,DF=EFDE=8x,
同理可得:△ADE≌△DPF,则AE=DF,即:2x12=8x,
解得x=![]() ,
,
∴2x+6=![]() ,
,
∴D(![]() ,
,![]() ),
),
此时,ED=PF=![]() ,AE=BF=
,AE=BF=![]() ,BP=PFBF=
,BP=PFBF=![]() <6,符合题意,
<6,符合题意,
综上所述,D点坐标为:(4,2)或(![]() ,
,![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
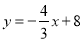 的图像与
的图像与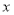 轴、
轴、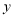 轴交于
轴交于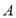 、
、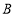 两点,
两点,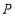 是
是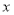 轴正半轴上的一个动点,连接
轴正半轴上的一个动点,连接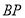 ,将
,将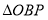 沿
沿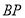 翻折,点
翻折,点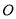 恰好落在
恰好落在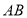 上,则点
上,则点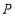 的坐标为______.
的坐标为______.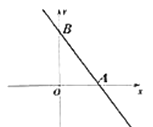
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
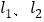 都与直线l垂直,垂足分别为M,N,MN=1,正方形ABCD的边长为
都与直线l垂直,垂足分别为M,N,MN=1,正方形ABCD的边长为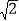 ,对角线AC在直线l上,且点C位于点M处,将正方形ABCD沿l向右平移,直到点A与点N重合为止,记点C平移的距离为x,正方形ABCD的边位于
,对角线AC在直线l上,且点C位于点M处,将正方形ABCD沿l向右平移,直到点A与点N重合为止,记点C平移的距离为x,正方形ABCD的边位于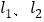 之间部分的长度和为y,则y关于x的函数图象大致为( )
之间部分的长度和为y,则y关于x的函数图象大致为( )
A.
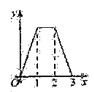 B.
B. 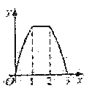 C.
C. 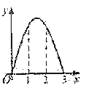 D.
D. 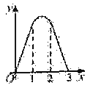
-
科目: 来源: 题型:
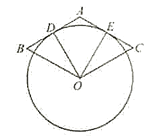
查看答案和解析>>【题目】如图,菱形ABOC的AB,AC分别与⊙O相切于点D、E,若点D是AB的中点,则∠DOE=__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车在笔直的公路上同起点、同方向、同终点匀速行驶
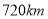 ,先到终点的人原地休息.已知甲先出发
,先到终点的人原地休息.已知甲先出发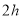 ,在整个过程中,甲、乙两车的距离
,在整个过程中,甲、乙两车的距离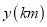 与甲出发的时间
与甲出发的时间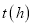 之间的关系如图所示.
之间的关系如图所示.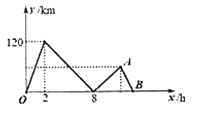
(1)甲的速度为______
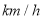 ,乙的速度为______
,乙的速度为______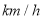 ;
;(2)说明
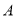 点表示的意义,求出
点表示的意义,求出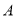 点坐标;
点坐标;(3)求出线段
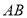 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;(4)甲出发多长时间两车相距
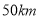 ,直接写出结果.
,直接写出结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线AB∥DC,点P为平面上一点,连接AP与CP.



(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,求∠APC.
(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
相关试题

