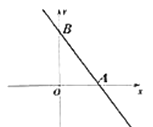
【题目】如图,一次函数![]() 的图像与
的图像与![]() 轴、
轴、![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() 是
是![]() 轴正半轴上的一个动点,连接
轴正半轴上的一个动点,连接![]() ,将
,将![]() 沿
沿![]() 翻折,点
翻折,点![]() 恰好落在
恰好落在![]() 上,则点
上,则点![]() 的坐标为______.
的坐标为______.
参考答案:
【答案】(![]() ,0)或(24,0)
,0)或(24,0)
【解析】
分两种情况讨论:当点P在OA上时,由O与C关于PB对称,可得OP=CP,BC=OB=8;当点P在AO延长线上时,由O与C关于PB对称,可得OP=CP,BC=OB=8,分别依据勾股定理得到方程,解方程即可得到点P的坐标.
解:设点O关于直线PB的对称点是C.
∵一次函数![]() 的图象与x轴、y轴交于A、B两点,
的图象与x轴、y轴交于A、B两点,
∴AO=6,BO=8,AB=10.
分两种情况:
①当点P在OA上时,
由折叠的性质,可得OP=CP,BC=OB=8,∠BCP=∠BOP=90°.
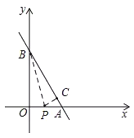
设OP=CP=x,则AP=6x,AC=108=2,
在Rt△ACP中,由勾股定理可得:x2+22=(6x)2,
解得x=![]() ,
,
∴P(![]() ,0);
,0);
②当点P在AO延长线上时,
由折叠的性质,可得OP=CP,BC=OB=8,∠C=∠BOP=90°.
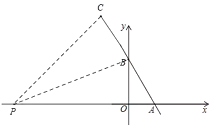
设OP=CP=x,则AP=6+x,AC=10+8=18,
在Rt△ACP中,由勾股定理可得:x2+182=(6+x)2,
解得x=24,
∴P(24,0).
故答案为:(![]() ,0)或(24,0).
,0)或(24,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数
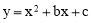 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.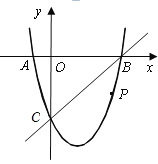
(1)求二次函数解析式;
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形
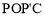 .是否存在点P,使四边形
.是否存在点P,使四边形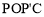 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
-
科目: 来源: 题型:
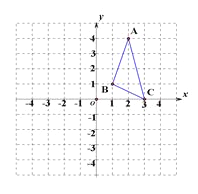
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的三个顶点的位置如图所示,将△ABC水平向左平移3个单位,再竖直向下平移2个单位。
(1)读出△ABC的三个顶点坐标;
(2)请画出平移后的△A′B′C′,并直接写出点A/、B′、C′的坐标;
(3)求平移以后的图形的面积 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
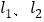 都与直线l垂直,垂足分别为M,N,MN=1,正方形ABCD的边长为
都与直线l垂直,垂足分别为M,N,MN=1,正方形ABCD的边长为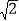 ,对角线AC在直线l上,且点C位于点M处,将正方形ABCD沿l向右平移,直到点A与点N重合为止,记点C平移的距离为x,正方形ABCD的边位于
,对角线AC在直线l上,且点C位于点M处,将正方形ABCD沿l向右平移,直到点A与点N重合为止,记点C平移的距离为x,正方形ABCD的边位于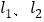 之间部分的长度和为y,则y关于x的函数图象大致为( )
之间部分的长度和为y,则y关于x的函数图象大致为( )
A.
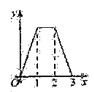 B.
B. 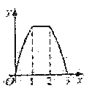 C.
C. 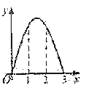 D.
D. 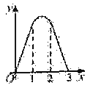
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABOC的AB,AC分别与⊙O相切于点D、E,若点D是AB的中点,则∠DOE=__________.
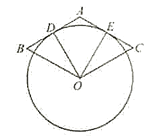
-
科目: 来源: 题型:
查看答案和解析>>【题目】(模型建立)
(1)如图1,等腰直角三角形
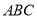 中,
中,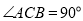 ,
,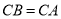 ,直线
,直线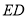 经过点
经过点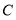 ,过
,过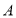 作
作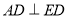 于点
于点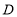 ,过
,过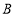 作
作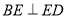 于点
于点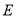 .求证:
.求证: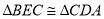 ;
;(模型应用)
(2)已知直线
 :
: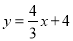 与坐标轴交于点
与坐标轴交于点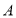 、
、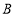 ,将直线
,将直线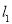 绕点
绕点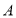 逆时针旋转
逆时针旋转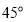 至直线
至直线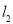 ,如图2,求直线
,如图2,求直线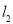 的函数表达式;
的函数表达式;(3)如图3,长方形
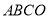 ,
,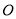 为坐标原点,点
为坐标原点,点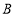 的坐标为
的坐标为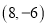 ,点
,点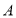 、
、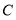 分别在坐标轴上,点
分别在坐标轴上,点 是线段
是线段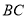 上的动点,点
上的动点,点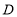 是直线
是直线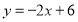 上的动点且在第四象限.若
上的动点且在第四象限.若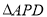 是以点
是以点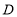 为直角顶点的等腰直角三角形,请直接写出点
为直角顶点的等腰直角三角形,请直接写出点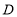 的坐标.
的坐标.
相关试题

