【题目】矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
参考答案:
【答案】3或1.2
【解析】由△PBE∽△DBC,可得∠PBE=∠DBC,继而可确定点P在BD上,然后再根据△APD是等腰三角形,分DP=DA、AP=DP两种情况进行讨论即可得.
∵四边形ABCD是矩形,∴∠BAD=∠C=90°,CD=AB=6,∴BD=10,
∵△PBE∽△DBC,
∴∠PBE=∠DBC,∴点P在BD上,
如图1,当DP=DA=8时,BP=2,
∵△PBE∽△DBC,
∴PE:CD=PB:DB=2:10,
∴PE:6=2:10,
∴PE=1.2;

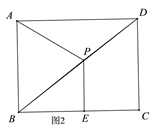
如图2,当AP=DP时,此时P为BD中点,
∵△PBE∽△DBC,
∴PE:CD=PB:DB=1:2,
∴PE:6=1:2,
∴PE=3;
综上,PE的长为1.2或3,
故答案为:1.2或3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(模型建立)
(1)如图1,等腰直角三角形
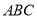 中,
中,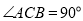 ,
,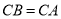 ,直线
,直线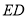 经过点
经过点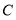 ,过
,过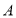 作
作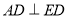 于点
于点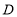 ,过
,过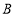 作
作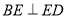 于点
于点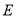 .求证:
.求证: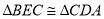 ;
;(模型应用)
(2)已知直线
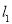 :
: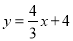 与坐标轴交于点
与坐标轴交于点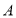 、
、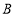 ,将直线
,将直线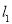 绕点
绕点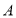 逆时针旋转
逆时针旋转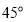 至直线
至直线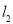 ,如图2,求直线
,如图2,求直线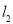 的函数表达式;
的函数表达式;(3)如图3,长方形
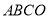 ,
,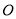 为坐标原点,点
为坐标原点,点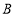 的坐标为
的坐标为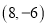 ,点
,点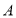 、
、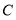 分别在坐标轴上,点
分别在坐标轴上,点 是线段
是线段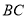 上的动点,点
上的动点,点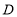 是直线
是直线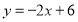 上的动点且在第四象限.若
上的动点且在第四象限.若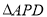 是以点
是以点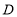 为直角顶点的等腰直角三角形,请直接写出点
为直角顶点的等腰直角三角形,请直接写出点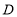 的坐标.
的坐标.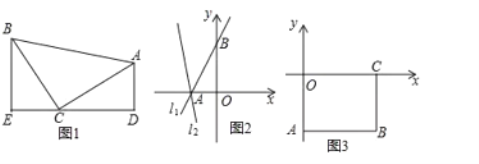
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车在笔直的公路上同起点、同方向、同终点匀速行驶
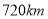 ,先到终点的人原地休息.已知甲先出发
,先到终点的人原地休息.已知甲先出发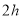 ,在整个过程中,甲、乙两车的距离
,在整个过程中,甲、乙两车的距离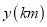 与甲出发的时间
与甲出发的时间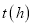 之间的关系如图所示.
之间的关系如图所示.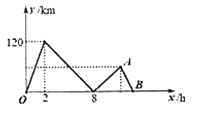
(1)甲的速度为______
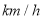 ,乙的速度为______
,乙的速度为______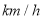 ;
;(2)说明
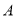 点表示的意义,求出
点表示的意义,求出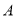 点坐标;
点坐标;(3)求出线段
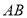 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;(4)甲出发多长时间两车相距
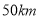 ,直接写出结果.
,直接写出结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线AB∥DC,点P为平面上一点,连接AP与CP.



(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,求∠APC.
(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在由边长为1个单位长度的小正方形组成的10×10网格中,已知点O,A,B均为网格线的交点.
(1)在给定的网格中,以点O为位似中心,将线段AB放大为原来的2倍,得到线段
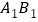 (点A,B的对应点分别为
(点A,B的对应点分别为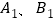 ).画出线段
).画出线段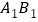 ;
;(2)将线段
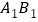 绕点
绕点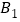 逆时针旋转90°得到线段
逆时针旋转90°得到线段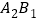 .画出线段
.画出线段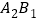 ;
;(3)以
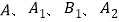 为顶点的四边形
为顶点的四边形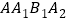 的面积是 个平方单位.
的面积是 个平方单位.
-
科目: 来源: 题型:
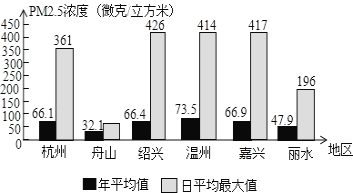
查看答案和解析>>【题目】2017年1月10日,绿色和平发布了全国74个城市PM2.5浓度年均值排名和相应的最大日均值,其中浙江省六个地区的浓度如下图所示(舟山的最大日均值条形图缺损)以下说法中错误的是______.
①则六个地区中,最大日均值最高的是绍兴;②杭州的年均值大约是舟山的2倍;③舟山的最大日均值不一定低于丽水的最大日均值;④六个地区中,低于国家环境空气质量标准规定的年均值35微克每立方米的地区只有舟山.
-
科目: 来源: 题型:
查看答案和解析>>【题目】自行车厂某周计划生产2100辆电动车,平均每天生产电动车300辆.由于各种原因,实际每天的生产量与计划每天的生产量相比有出入,下表是该周的实际生产情况(超产记为正、减产记为负,单位:辆):
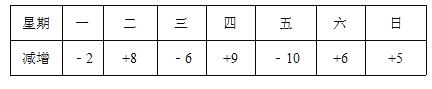
(1)该厂星期一生产电动车 辆;
(2)生产量最多的一天比生产量最少的一天多生产电动车 辆;
(3)该厂实行记件工资制,每生产一辆车可得60元,那么该厂工人这一周的工资总额是多少元?
相关试题

