【题目】如图1,在![]() 中,
中,![]() 是BC上的一点,以AD为边作
是BC上的一点,以AD为边作![]() ,使
,使![]() .
.
(1)直接用含![]() 的式子表示
的式子表示![]() 的度数是_______________;
的度数是_______________;
(2)以![]() 为边作平行四边形
为边作平行四边形![]() ;
;
①如图2,若点F恰好落在DE上,试判断线段BD与线段CD的长度是否相等,并说明理由.
②如图3,若点F落在是DE上,且![]() ,求线段CF的长(直接写出结果,不说明理由).
,求线段CF的长(直接写出结果,不说明理由).

参考答案:
【答案】(1)![]() ;(2)①相等,见解析,②
;(2)①相等,见解析,②![]()
【解析】
(1)由在△ABC中,AB=AC,∠ABC=α,可求得∠BAC=180°2α,又由AE=AD,∠DAE+∠BAC=180°,可求得∠DAE=2α,继而求得∠ADE的度数;
(2)①由四边形ABFE是平行四边形,易得∠EDC=∠ABC=α,则可得∠ADC=∠ADE+∠EDC=90°,证得AD⊥BC,又由AB=AC,根据三线合一的性质,即可证得结论;
②由在△ABC中,AB=AC,∠ABC=α,可得∠B=∠C=α,四边形ABFE是平行四边形,可得AE∥BF,AE=BF.即可证得:∠EAC=∠C=α,又由(1)可证得AD=CD,又由AD=AE=BF,证得结论.
(1)∵在△ABC中,AB=AC,∠ABC=α,
∴∠BAC=180°2α,
∵∠DAE+∠BAC=180°,
∴∠DAE=2α,
∵AE=AD,
∴∠ADE=90°α;
故答案为:90°α;
(2)①证明:∵四边形ABFE是平行四边形,
∴AB∥EF.
∴∠EDC=∠ABC=α,
由(1)知,∠ADE=90°α,
∴∠ADC=∠ADE+∠EDC=90°,
∴AD⊥BC.
∵AB=AC,
∴BD=CD;
②证明:∵AB=AC,∠ABC=α,
∴∠C=∠B=α.
∵四边形ABFE是平行四边形,
∴AE∥BF,AE=BF.
∴∠EAC=∠C=α,
由(1)知,∠DAE=2α,
∴∠DAC=α,
∴∠DAC=∠C.
∴AD=CD.
∵AD=AE=BF,
∴BF=CD.
∴BD=CF.
∴![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图E是平行四边形
 边BC上一点,且
边BC上一点,且 ,连接AE,并延长AE与DC的延长线交于点F,
,连接AE,并延长AE与DC的延长线交于点F,  .
.(1)请判断
 的形状,并说明理由;
的形状,并说明理由;(2)求
 的各内角的大小.
的各内角的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在用描点法画二次函数y=ax2+bx+c图象时,由于粗心,他算错了一个y值,列出了下面表格:
x
…
﹣1
0
1
2
3
…
y=ax2+bx+c
…
5
3
2
3
6
…
(1)请指出这个错误的y值,并说明理由;
(2)若点M(a,y1),N(a+4,y2)在二次函数y=ax2+bx+c图象上,且a>﹣1,试比较y1与y2的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校兴趣小组,对函数y=|x﹣1|+1的图像和性质进行了研究,探究过程如下:
(1)自变量
 的取值范围是全体实数,
的取值范围是全体实数, 与
与 的几组对应值如表:
的几组对应值如表:X
……



0
1
2
3
4
5
……
y
……
5
4
m
2
1
2
3
4
5
……
其中

(2)在平面直角坐标系中,画出上表中对应值为点的坐标,根据画出的点,画出该函数的图象;

(3)根据画出的函数图像特征,仿照示例,完成下表中函数的变化规律:
序号
函数图像特征
函数变化规律
示例1
在直线
 的右侧,函数图像自左至右呈上升趋势
的右侧,函数图像自左至右呈上升趋势当
 时y随x的增大而增大
时y随x的增大而增大①
在直线
 的右侧,函数图像自左至右呈下降趋势
的右侧,函数图像自左至右呈下降趋势
示例2
函数图像经过点(-3,5)
当
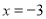 时
时
②
函数图像的最低点是

当
 时,函数有最
时,函数有最 (大或小)值,此时
(大或小)值,此时
(4)当
 时,
时, 的取值范围是_____________
的取值范围是_____________ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(4,3)是反比例函数y=
 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y= 的图象于点P.
的图象于点P.(1)求反比例函数y=
 的表达式;
的表达式;(2)求点B的坐标;
(3)求△OAP的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB⊥AC,AB=2,AC=4.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转α°,分别交直线BC、AD于点E、F.

(1)当α= °,四边形ABEF是平行四边形;
(2)在旋转的过程中,从A、B、C、D、E、F中任意4个点为顶点构造四边形.
①α= °,构造的四边形是菱形;
②若构造的四边形是矩形,求出该矩形的面积.
相关试题

