【题目】如图,梯形ABCD上底的长是4,下底的长是x,高是6.
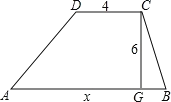
(1)求梯形ABCD的面积y与下底长x之间的关系式;
(2)用表格表示当x从10变到16时(每次增加1),y的相应值;
(3)x每增加1时,y如何变化?说明你的理由.
参考答案:
【答案】(1)y=![]() (4+x)×6=12﹣3x;(2)表格见解析;(3)由上表可得:x每增加1时,y减小3,理由见解析.
(4+x)×6=12﹣3x;(2)表格见解析;(3)由上表可得:x每增加1时,y减小3,理由见解析.
【解析】(1)利用梯形面积公式得出y与x 之间的关系;(2)结合关系式列表计算得出相关数据;(3)利用(1)中关系式,进而得出x每增加1时,y的变化.
解:(1)∵梯形ABCD上底的长是4,下底的长是x,高是6,
∴梯形ABCD的面积y与下底长x之间的关系式为:y=![]() (4+x)×6=12﹣3x;
(4+x)×6=12﹣3x;
(2)表格如下:
x | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
y | ﹣18 | ﹣21 | ﹣24 | ﹣27 | ﹣30 | ﹣33 | ﹣36 |
(3)由上表可得:x每增加1时,y减小3,
理由:y1=12﹣3x,y2=12﹣3(x+1)=12﹣3x﹣3=9﹣3x,
y2﹣y1=9﹣3x﹣(12﹣3x)=﹣3,即x每增加1时,y减小3.
“点睛”此题主要考查了函数关系式以及函数的变化,正确得出函数关系式是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边为
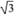 的正方形ABCD绕点A沿逆时针方向旋转30°后得到正方形AEFH,则图中阴影部分的面积为( )
的正方形ABCD绕点A沿逆时针方向旋转30°后得到正方形AEFH,则图中阴影部分的面积为( )
A.
 -
- B. 3-
B. 3-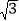 C. 2-
C. 2-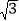 D. 2-
D. 2-
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校有一块长为(5a+b)米,宽为(3a+b)米的长方形空地,中间是边长(a﹣b)米的正方形草坪,其余为活动场地,学校计划将活动场地(阴影部分)进行硬化.
(1)用含a,b的代数式表示需要硬化的面积并化简;
(2)当a=5,b=2时,求需要硬化的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)|﹣3|+(﹣1)2016×(π﹣3.14)0﹣(
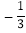 )﹣2+2﹣3
)﹣2+2﹣3(2)利用乘法公式计算:20182﹣2017×2019
(3)已知2a=3,4b=5,8c=7,求8a+c﹣2b的值.
(4)已知x2﹣5x=14,求(x﹣1)(2x﹣1)﹣(x+1)2+1的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,直线EF与AB、CD分别相交于E、F两点,EP平分∠AEF,过点F作FP⊥EP,若∠PEF=30°,则∠PFC等于( )
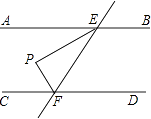
A.30°
B.45°
C.60°
D.120° -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程
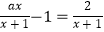 的解为非正数,且关于x的不等式组
的解为非正数,且关于x的不等式组 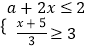 无解,那么满足条件的所有整数a的和是( )
无解,那么满足条件的所有整数a的和是( )
A.﹣19
B.﹣15
C.﹣13
D.﹣9 -
科目: 来源: 题型:
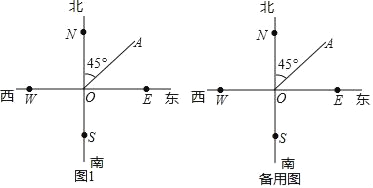
查看答案和解析>>【题目】如图,射线ON、OE、OS、OW分别表示从点O出发北、东、南、西四个方向,点A在点O的北偏东45°方向,点B在点O的北偏西30°方向.
(1)画出射线OB,若∠BOC与∠AOB互余,请在图1或备用图中画出∠BOC;
(2)若OP是∠AOC的角平分线,直接写出∠AOP的度数(不需要计算过程).
相关试题

