【题目】如图,AB∥CD,直线EF与AB、CD分别相交于E、F两点,EP平分∠AEF,过点F作FP⊥EP,若∠PEF=30°,则∠PFC等于( )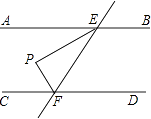
A.30°
B.45°
C.60°
D.120°
参考答案:
【答案】C
【解析】解:∵EP平分∠AEF,∠PEF=30°,
∴∠AEF=2∠PEF=60°,
∵AB∥CD,
∴∠CFE=180°﹣∠AEF=120°,
∵FP⊥EP,
∴∠P=90°,
∵∠PEF=30°,
∴∠PFE=60°,
∴∠PFC=∠CFE﹣∠PFE=120°﹣60°=60°.
所以答案是:C.
【考点精析】掌握垂线的性质和平行线的性质是解答本题的根本,需要知道垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短;两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校有一块长为(5a+b)米,宽为(3a+b)米的长方形空地,中间是边长(a﹣b)米的正方形草坪,其余为活动场地,学校计划将活动场地(阴影部分)进行硬化.
(1)用含a,b的代数式表示需要硬化的面积并化简;
(2)当a=5,b=2时,求需要硬化的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)|﹣3|+(﹣1)2016×(π﹣3.14)0﹣(
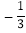 )﹣2+2﹣3
)﹣2+2﹣3(2)利用乘法公式计算:20182﹣2017×2019
(3)已知2a=3,4b=5,8c=7,求8a+c﹣2b的值.
(4)已知x2﹣5x=14,求(x﹣1)(2x﹣1)﹣(x+1)2+1的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形ABCD上底的长是4,下底的长是x,高是6.
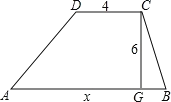
(1)求梯形ABCD的面积y与下底长x之间的关系式;
(2)用表格表示当x从10变到16时(每次增加1),y的相应值;
(3)x每增加1时,y如何变化?说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程
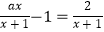 的解为非正数,且关于x的不等式组
的解为非正数,且关于x的不等式组 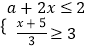 无解,那么满足条件的所有整数a的和是( )
无解,那么满足条件的所有整数a的和是( )
A.﹣19
B.﹣15
C.﹣13
D.﹣9 -
科目: 来源: 题型:
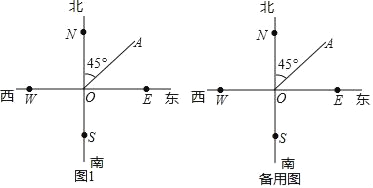
查看答案和解析>>【题目】如图,射线ON、OE、OS、OW分别表示从点O出发北、东、南、西四个方向,点A在点O的北偏东45°方向,点B在点O的北偏西30°方向.
(1)画出射线OB,若∠BOC与∠AOB互余,请在图1或备用图中画出∠BOC;
(2)若OP是∠AOC的角平分线,直接写出∠AOP的度数(不需要计算过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②2a+b>0;③y随x的增大而增大;④a﹣b+c<0,其中正确的个数( )
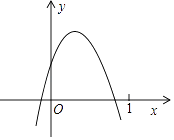
A.4个
B.3个
C.2个
D.1个
相关试题

