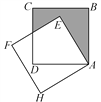
【题目】如图,将边为![]() 的正方形ABCD绕点A沿逆时针方向旋转30°后得到正方形AEFH,则图中阴影部分的面积为( )
的正方形ABCD绕点A沿逆时针方向旋转30°后得到正方形AEFH,则图中阴影部分的面积为( )
A. ![]() -
-![]() B. 3-
B. 3-![]() C. 2-
C. 2-![]() D. 2-
D. 2-![]()
参考答案:
【答案】B
【解析】分析:连接AG,根据∠BAE=30°可知∠DAE=60°,由正方形的性质可知,AB=AD,由图形旋转的性质可知AD=AE,故可得出Rt△ADG≌Rt△AEG,由直角三角形的性质可得出DG的长,再由S 阴影=![]() ,即可得出结论.
,即可得出结论.
本题解析:

连接AG,
∵∠BAE=30°,
∴∠DAE=60°,
∵四边形ABCD是正方形,
∴AB=AD,∠D=∠B=90°,
∵正方形AEFH是正方形ABCD旋转而成,
∴AD=AE,∠E=90°,
在Rt△ADG与Rt△AEG中,AD=AE,AG=AG,
∴Rt△ADG≌Rt△AEG,
∴∠DAG= ∠EAG =30°,
∴DG=ADtan∠DAG=![]() ×
×![]() =1,
=1,
∴![]()
∴S 四边形ADGE=2![]() =2×
=2×![]() =
=![]() ,
,
∴S 阴影=![]() ,故选B.
,故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一块长与宽之比为2∶1的铁皮的四角各剪去一个边长为10 cm的小正方形,折起四边,可以做成一个无盖的盒子.如果这个盒子的容积是1 500 cm3,那么铁皮的长和宽各是多少?若设铁皮的宽为x cm,则正确的方程是( )
A. (2x-20)(x-20)=1 500 B. (2x-10)(x-20)=1 500
C. 10(2x-20)(x-20)=1 500 D. 10(x-10)(x-20)=1 500
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果n边形每一个内角等于与它相邻外角的2倍,则n的值是( )
A. 4 B. 5 C. 6 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句描述的事件中,是不可能事件的是( )
A. 只手遮天,偷天换日B. 心想事成,万事如意
C. 瓜熟蒂落,水到渠成D. 水能载舟,亦能覆舟
-
科目: 来源: 题型:
查看答案和解析>>【题目】火车匀速通过隧道时,火车在隧道内的长度
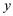 (米)与火车行驶时间
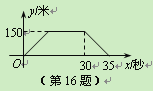
(米)与火车行驶时间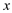 (秒)之间的关系用图象描述如图所示,有下列结论:
(秒)之间的关系用图象描述如图所示,有下列结论:①火车的长度为120米;
②火车的速度为30米/秒;
③火车整体都在隧道内的时间为25秒;
④隧道长度为750米.
其中正确的结论是 .(把你认为正确结论的序号都填上)
-
科目: 来源: 题型:
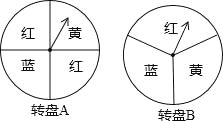
查看答案和解析>>【题目】小明、小亮做一个“配色”的游戏.下图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色.同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,或者转盘A转出了蓝色,转盘B转出了红色,则红色和蓝色在一起配成紫色.这种情况下小亮得1分;同样,蓝色和黄色在一起配成绿色,这种情况下小明得1分;在其它情况下,则小明、小亮不分胜负.这个游戏对双方公平吗?请说明理由.若不公平,如何修改游戏规则才能使游戏对双方公平?
-
科目: 来源: 题型:
查看答案和解析>>【题目】货主两次租用某汽车运输公司的甲,乙两种货车运送货物往某地,第一次租用甲货车2辆和乙货车3辆共运送15.5吨货物,第二次租用甲货车3辆和乙货车2辆共运送17吨货物,两次运输都按货车的最大核定载货量刚好将货物运送完,没有超载.
(1)求甲,乙两种货车每辆最大核定载货量是多少吨?
(2)已知租用甲种货车运费为每辆1200元,租用乙种货车运费为每辆800元,现在货主有24吨货物需要运送,而汽车运输公司只有2辆甲种货车,其它的都是乙种货车,问有几种租车方案?哪种方案费用较少?
相关试题

