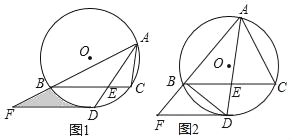
【题目】如图1,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交BC于点E(BE>EC),且BD=2![]() .过点D作DF∥BC,交AB的延长线于点F.
.过点D作DF∥BC,交AB的延长线于点F.
(1)求证:DF为⊙O的切线;
(2)若∠BAC=60°,DE=![]() ,求图中阴影部分的面积;
,求图中阴影部分的面积;
(3)若![]() ,DF+BF=8,如图2,求BF的长.
,DF+BF=8,如图2,求BF的长.
参考答案:
【答案】(1)证明见解析(2)9![]() ﹣2π;(3)3
﹣2π;(3)3
【解析】试题分析:(1)连结OD,如图1,由已知得到∠BAD=∠CAD,得到![]() ,再由垂径定理得OD⊥BC,由于BC∥EF,则OD⊥DF,于是可得结论;
,再由垂径定理得OD⊥BC,由于BC∥EF,则OD⊥DF,于是可得结论;
(2)连结OB,OD交BC于P,作BH⊥DF于H,如图1,先证明△OBD为等边三角形得到∠ODB=60°,OB=BD=![]() ,得到∠BDF=∠DBP=30°,在Rt△DBP中得到PD=
,得到∠BDF=∠DBP=30°,在Rt△DBP中得到PD=![]() ,PB=3,在Rt△DEP中利用勾股定理可算出PE=2,由于OP⊥BC,则BP=CP=3,得到CE=1,由△BDE∽△ACE,得到AE的长,再证明△ABE∽△AFD,可得DF=12,最后利用S阴影部分=S△BDF﹣S弓形BD=S△BDF﹣(S扇形BOD﹣S△BOD)进行计算;
,PB=3,在Rt△DEP中利用勾股定理可算出PE=2,由于OP⊥BC,则BP=CP=3,得到CE=1,由△BDE∽△ACE,得到AE的长,再证明△ABE∽△AFD,可得DF=12,最后利用S阴影部分=S△BDF﹣S弓形BD=S△BDF﹣(S扇形BOD﹣S△BOD)进行计算;
(3)连结CD,如图2,由![]() 可设AB=4x,AC=3x,设BF=y,由
可设AB=4x,AC=3x,设BF=y,由![]() 得到CD=BD=
得到CD=BD=![]() ,由△BFD∽△CDA,得到xy=4,再由△FDB∽△FAD,得到16﹣4y=xy,则16﹣4y=4,然后解方程即可得到BF=3.
,由△BFD∽△CDA,得到xy=4,再由△FDB∽△FAD,得到16﹣4y=xy,则16﹣4y=4,然后解方程即可得到BF=3.
试题解析:(1)连结OD,如图1,∵AD平分∠BAC交⊙O于D,∴∠BAD=∠CAD,∴![]() ,∴OD⊥BC,∵BC∥EF,∴OD⊥DF,∴DF为⊙O的切线;
,∴OD⊥BC,∵BC∥EF,∴OD⊥DF,∴DF为⊙O的切线;
(2)连结OB,连结OD交BC于P,作BH⊥DF于H,如图1,∵∠BAC=60°,AD平分∠BAC,∴∠BAD=30°,∴∠BOD=2∠BAD=60°,∴△OBD为等边三角形,∴∠ODB=60°,OB=BD=![]() ,∴∠BDF=30°,∵BC∥DF,∴∠DBP=30°,在Rt△DBP中,PD=
,∴∠BDF=30°,∵BC∥DF,∴∠DBP=30°,在Rt△DBP中,PD=![]() BD=
BD=![]() ,PB=
,PB=![]() PD=3,在Rt△DEP中,∵PD=
PD=3,在Rt△DEP中,∵PD=![]() ,DE=
,DE=![]() ,∴PE=
,∴PE=![]() =2,∵OP⊥BC,∴BP=CP=3,∴CE=3﹣2=1,易证得△BDE∽△ACE,∴AE:BE=CE:DE,即AE:5=1:
=2,∵OP⊥BC,∴BP=CP=3,∴CE=3﹣2=1,易证得△BDE∽△ACE,∴AE:BE=CE:DE,即AE:5=1: ![]() ,∴AE=
,∴AE=![]() ,∵BE∥DF,∴△ABE∽△AFD,∴
,∵BE∥DF,∴△ABE∽△AFD,∴![]() ,即
,即 ,解得DF=12,在Rt△BDH中,BH=
,解得DF=12,在Rt△BDH中,BH=![]() BD=
BD=![]() ,∴S阴影部分=S△BDF﹣S弓形BD=S△BDF﹣(S扇形BOD﹣S△BOD)=
,∴S阴影部分=S△BDF﹣S弓形BD=S△BDF﹣(S扇形BOD﹣S△BOD)= =
=![]() ;
;
(3)连结CD,如图2,由![]() 可设AB=4x,AC=3x,设BF=y,∵
可设AB=4x,AC=3x,设BF=y,∵![]() ,∴CD=BD=
,∴CD=BD=![]() ,∵∠F=∠ABC=∠ADC,∵∠FDB=∠DBC=∠DAC,∴△BFD∽△CDA,∴
,∵∠F=∠ABC=∠ADC,∵∠FDB=∠DBC=∠DAC,∴△BFD∽△CDA,∴![]() ,即
,即![]() ,∴xy=4,∵∠FDB=∠DBC=∠DAC=∠FAD,而∠DFB=∠AFD,∴△FDB∽△FAD,∴
,∴xy=4,∵∠FDB=∠DBC=∠DAC=∠FAD,而∠DFB=∠AFD,∴△FDB∽△FAD,∴![]() ,即
,即![]() ,整理得16﹣4y=xy,∴16﹣4y=4,解得y=3,即BF的长为3.
,整理得16﹣4y=xy,∴16﹣4y=4,解得y=3,即BF的长为3.

-
科目: 来源: 题型:
查看答案和解析>>【题目】体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
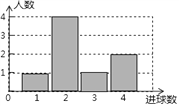
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天早晨,小王从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是小王从家到学校这一过程中所走的路程 s(米)与时间 t(分)之间的关系.
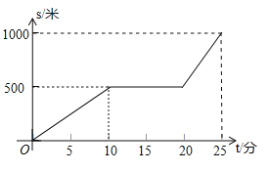
(1)小王从家到学校的路程共_________米,从家出发到学校,小王共用了________分钟;
(2)小王吃早餐用了____________分钟;
(3)小王吃早餐以前和吃完早餐后的平均速度分别是多少米/分钟?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆柱形玻璃杯,高为
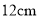 ,底面周长为
,底面周长为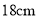 ,在杯内离杯底
,在杯内离杯底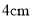 的点
的点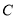 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿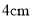 与蜂蜜相对的点
与蜂蜜相对的点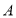 处,则蚂蚁到达蜂蜜的最短距离为( )
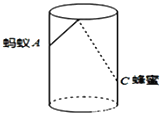
处,则蚂蚁到达蜂蜜的最短距离为( )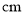 .
.
A. 15B.
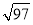 C. 12D. 18
C. 12D. 18 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(0,2
 ),动点B、C从原点O同时出发,分别以每秒1个单位和每秒2个单位长度的速度沿x轴正方向运动,以点A为圆心,OB的长为半径画圆;以BC为一边,在x轴上方作等边△BCD.设运动的时间为t秒,当⊙A与△BCD的边BD所在直线相切时,t的值为( )
),动点B、C从原点O同时出发,分别以每秒1个单位和每秒2个单位长度的速度沿x轴正方向运动,以点A为圆心,OB的长为半径画圆;以BC为一边,在x轴上方作等边△BCD.设运动的时间为t秒,当⊙A与△BCD的边BD所在直线相切时,t的值为( )
A.
 B.
B.  C. 4
C. 4 +6 D. 4
+6 D. 4 -6
-6 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=kx+b经过点A(3,7)和B(﹣8,-4).
(1)求直线的解析式;
(2)求出该直线与x轴、y轴的交点坐标。并求出直线与两坐标轴围成三角形的面积。
-
科目: 来源: 题型:
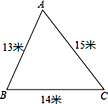
查看答案和解析>>【题目】某小区内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化小区环境,预计花园每平方米造价为25元,小区修建这个花园需要投资多少元?
相关试题

