【题目】如图,在平面直角坐标系中,A(0,2![]() ),动点B、C从原点O同时出发,分别以每秒1个单位和每秒2个单位长度的速度沿x轴正方向运动,以点A为圆心,OB的长为半径画圆;以BC为一边,在x轴上方作等边△BCD.设运动的时间为t秒,当⊙A与△BCD的边BD所在直线相切时,t的值为( )
),动点B、C从原点O同时出发,分别以每秒1个单位和每秒2个单位长度的速度沿x轴正方向运动,以点A为圆心,OB的长为半径画圆;以BC为一边,在x轴上方作等边△BCD.设运动的时间为t秒,当⊙A与△BCD的边BD所在直线相切时,t的值为( )

A. ![]() B.
B. ![]() C. 4
C. 4![]() +6 D. 4
+6 D. 4![]() -6
-6
参考答案:
【答案】C
【解析】分析:如图所示,根据题意画出图形,并作矩形OGEF,先证Rt△AOB≌Rt△BEA,再证△BEF是含有30°角的三角形,从而求出BF与EF的长,最后在Rt△AGE中利用勾股定理建立含t的方程,解方程即可得出答案.
详解:当点B运动到如图所示的位置时,⊙A与边BD所在直线相切,切点为E,
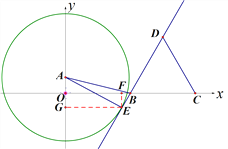
作EF⊥x轴,垂足为F,作EG⊥y轴,垂足为G,可得矩形OGEF,
在Rt△AOB与Rt△BEA中,
![]()
∴Rt△AOB≌Rt△BEA,
∴BE=AO=2![]() ,
,
∵△BCD是等边三角形,
∴∠DBC=60°,
∴∠FBE=∠DBC=60°,
∵∠BFE=90°,
∴∠BEF=30°,
∴BF=![]() ,EF=3,
,EF=3,
∴GE=t-![]() ,AG=2
,AG=2![]() +3,
+3,
在Rt△AGE中,由勾股定理得,
AG2+GE2=AE2,
即![]() ,
,
解得,![]() .
.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天早晨,小王从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是小王从家到学校这一过程中所走的路程 s(米)与时间 t(分)之间的关系.
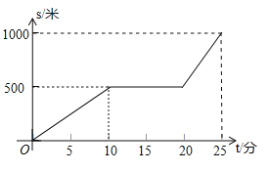
(1)小王从家到学校的路程共_________米,从家出发到学校,小王共用了________分钟;
(2)小王吃早餐用了____________分钟;
(3)小王吃早餐以前和吃完早餐后的平均速度分别是多少米/分钟?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆柱形玻璃杯,高为
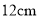 ,底面周长为
,底面周长为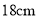 ,在杯内离杯底
,在杯内离杯底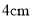 的点
的点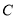 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿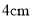 与蜂蜜相对的点
与蜂蜜相对的点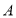 处,则蚂蚁到达蜂蜜的最短距离为( )
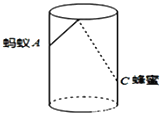
处,则蚂蚁到达蜂蜜的最短距离为( )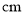 .
.
A. 15B.
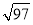 C. 12D. 18
C. 12D. 18 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交BC于点E(BE>EC),且BD=2
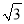 .过点D作DF∥BC,交AB的延长线于点F.
.过点D作DF∥BC,交AB的延长线于点F.(1)求证:DF为⊙O的切线;
(2)若∠BAC=60°,DE=
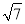 ,求图中阴影部分的面积;
,求图中阴影部分的面积;(3)若
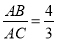 ,DF+BF=8,如图2,求BF的长.
,DF+BF=8,如图2,求BF的长.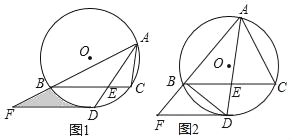
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=kx+b经过点A(3,7)和B(﹣8,-4).
(1)求直线的解析式;
(2)求出该直线与x轴、y轴的交点坐标。并求出直线与两坐标轴围成三角形的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化小区环境,预计花园每平方米造价为25元,小区修建这个花园需要投资多少元?
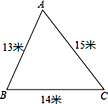
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,b满足
 +(c-7)2=0.
+(c-7)2=0.(1) a= ,b= ,c= .
(2) 若将数轴折叠,使得A点与C点重合,则点B与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= ,BC= .(用含t的代数式表示)
(4) 请问:3BC-2AB的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.

相关试题

