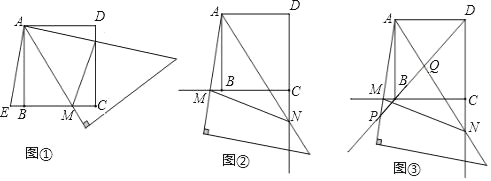
【题目】已知等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合,将此三角板绕A点旋转时,两边分别交直线BC,CD于点M、N.
(1)如图①,当M、N分别在边BC,CD上时,作AE垂直于AN,交CB的延长线于点E,求证:△ABE≌△ADN;
(2)如图②,当M、N分别在边CB,DC的延长线上时,求证:MN+BM=DN;
(3)如图③,当M、N分别在边CB,DC的延长线上时,作直线BD交直线AM、AN于P、Q两点,若MN=10,CM=8,求AP的长.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】试题分析:![]() 由同角的余角相等得到一对锐角相等,再由一对直角相等,又正方形的边长相等,利用ASA即可得到
由同角的余角相等得到一对锐角相等,再由一对直角相等,又正方形的边长相等,利用ASA即可得到![]() ≌
≌![]()
![]() 在
在![]() 上截取
上截取![]() 连接
连接![]() 首先证明
首先证明![]() ≌
≌![]() 再证
再证![]() 为等腰直角三角形,即可得到结论;
为等腰直角三角形,即可得到结论;
![]() 连接AC,在
连接AC,在![]() 中,由MN和CM的长,利用勾股定理求出CN的长,根据图3的结论等量代换即可求出BC的长,从而利用勾股定理求出AC的长,证明
中,由MN和CM的长,利用勾股定理求出CN的长,根据图3的结论等量代换即可求出BC的长,从而利用勾股定理求出AC的长,证明![]() 且相似比为
且相似比为![]() 在
在![]() 中,利用勾股定理求出AN的长,代入比例式即可求出AP的长.
中,利用勾股定理求出AN的长,代入比例式即可求出AP的长.
试题解析:![]() 如图1,
如图1,
∵AE垂直于AN,
![]()
∵四边形ABCD是正方形,
![]() ,
,
![]()
![]()
又![]()
∴![]() ≌
≌![]() (ASA);
(ASA);
(2)证明:如图②,在![]() 上截取
上截取![]() 连接
连接![]()
![]()
![]()
∴![]() ≌
≌![]()
![]()
![]()
![]()
![]() 为等腰直角三角形,
为等腰直角三角形,
![]()
∴AN为MG的垂直平分线,
![]()
![]() ,即
,即![]()
(3)如图③,连接AC,同(2),证得
![]()
![]()
![]()
即![]()
即![]() ,
,
在![]() 中,
中,
根据勾股定理得![]() 即
即![]()
![]()
![]()
![]()
![]()
![]()
又![]()
![]()
![]()
在![]() 中,
中,
根据勾股定理得![]()
解得![]()
![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
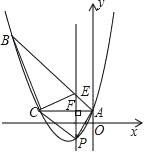
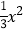 +bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB,AC分别交于点E,F,当四边形AECP的面积最大时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.

(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两点的坐标分别为(6,0),(0,6),点P从点A出发,沿AB方向以每秒
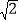 个单位的速度向终点B运动;同时动点Q从点B出发沿BO方向以每秒1个单位的速度向终点Q运动,将△PQO沿BO翻折,点P的对应点为点C,若四边形QPOC为菱形,则点C的坐标为________.
个单位的速度向终点B运动;同时动点Q从点B出发沿BO方向以每秒1个单位的速度向终点Q运动,将△PQO沿BO翻折,点P的对应点为点C,若四边形QPOC为菱形,则点C的坐标为________.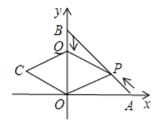
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的推理.
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,试说明:AB∥CD.

完成推理过程:
∵BE平分∠ABD(已知),
∴∠ABD=2∠α(__________).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (__________).
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( __________).
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(__________).
∴AB∥CD(____________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】去年4月,国民体质监测中心等机构开展了青少年形体测评,专家组随机抽查了某市若干名初中生坐姿、站姿、走姿的好坏情况. 我们对专家的测评数据作了适当处理(如果一个学生有一种以上不良姿势,我们以他最突出的一种作记载),并将统计结果绘制成了如下两幅不完整的统计图,请你根据图中所给信息解答些列问题:

(1)请将两幅图补充完整;
(2)在这次形体测评中,一共抽查了______名学生,如果全市有20万名初中生,那么全市初中生中,三姿良好的学生约有______人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=2x-2的图像与反比例函数y=
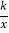 的图像交于点M(2,a)与N(b,-4)两点。
的图像交于点M(2,a)与N(b,-4)两点。(1)求反比例函数的解析式.
(2)画出草图,根据图像写出反比例函数的值大于一次函数的值时的x的取值范围.
(3)求△MON的面积.
相关试题

