【题目】如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A,C分别落在点A′、C′处,并且点A′,C′,B在同一条直线上,则tan∠ABA′的值为 . 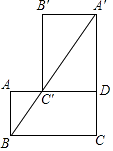
参考答案:
【答案】![]()
【解析】解: ∵四边形ABCD是矩形,
∴AD=BC=2,∠A=90°,C'D∥BC,
∵将矩形ABCD绕点D顺时针旋转90°,
∴AB=C'D,BC=B'C'=AD=2,
设AB=x,则AB=C'D=x,A'C=A'D+CD=x+2,
∵C'D∥BC,
∴△AC'D∽△ABC,
∴C'D:BC=AD:DC,
即x:2=2:x+2,
解得:x=﹣1+ ![]() 或x=﹣1﹣
或x=﹣1﹣ ![]() (小于0,不合题意,舍去),
(小于0,不合题意,舍去),
∴AC'=2﹣C'D=2﹣(﹣1+ ![]() )=3﹣
)=3﹣ ![]()
∴tan∠ABA′= ![]() =
= ![]() =
= ![]() ,
,
所以答案是: ![]() .
.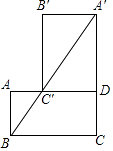
【考点精析】利用矩形的性质和解直角三角形对题目进行判断即可得到答案,需要熟知矩形的四个角都是直角,矩形的对角线相等;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
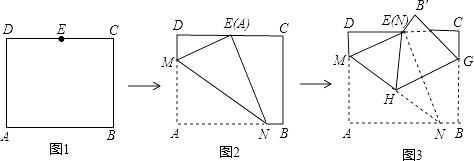
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8
 ,AD=10,点E是CD的中点,将这张纸片依次折叠两次:第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则下列结论正确的个数是( ) ①ME∥HG;②△MEH是等边三角形;③∠EHG=∠AMN;④tan∠EHG=
,AD=10,点E是CD的中点,将这张纸片依次折叠两次:第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则下列结论正确的个数是( ) ①ME∥HG;②△MEH是等边三角形;③∠EHG=∠AMN;④tan∠EHG= 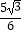
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD平移后得到四边形A′B′C′D′
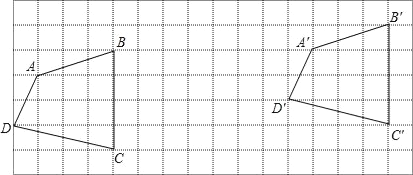
观察图形后完成下列问题:
(1)四边形ABCD先向 平移 个格,再向 平移 个格后得到四边形A′B′C′D′.
(2)图中有哪些相等的线段?有哪些平行的线段?
(3)S四边形ABCD和S四边形A′B′C′D′有什么关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2=50°,EF∥DB.
(1)DG与AB平行吗?请说明理由.
(2)若EC平分∠FED,求∠C的度数.
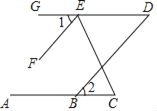
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有甲、乙两个瓷器店出售茶壶和茶杯,茶壶每只价格为20元,茶杯每只价格为5元,已知甲店制定的优惠方法是买一只茶壶送一只茶杯,乙店按总价的92%付款.学校办公室需要购买茶壶4只,茶杯若干只(不少于4只).
(1)当购买多少只茶杯时,两店的优惠方法付款一样多?
(2)当需要购买40只茶杯时,若让你去办这件事,你打算去哪家商店购买?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示已知
 ,
,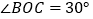 ,OM平分
,OM平分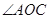 ,ON平分
,ON平分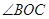 ;
;(1)
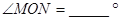 ;
;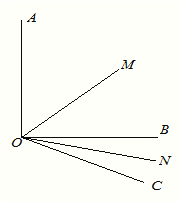
(2)如图∠AOB=900,将OC绕O点向下旋转,使∠BOC=
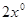 ,仍然分别作∠AOC,∠BOC的平分线OM,ON,能否求出∠MON的度数,若能,求出其值,若不能,试说明理由.
,仍然分别作∠AOC,∠BOC的平分线OM,ON,能否求出∠MON的度数,若能,求出其值,若不能,试说明理由.
(3)
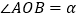 ,
,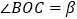 ,仍然分别作∠AOC,∠BOC的平分线OM,ON,能否求出∠MON的度数,若能,求
,仍然分别作∠AOC,∠BOC的平分线OM,ON,能否求出∠MON的度数,若能,求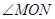 的度数;并从你的求解中看出什么什么规律吗?
的度数;并从你的求解中看出什么什么规律吗?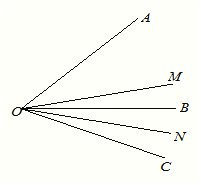
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1 , l2 , 过点(1,0)作x轴的垂线交l1于点A1 , 过点A1作y轴的垂线交l2于点A2 , 过点A2作x轴的垂线交l1于点A3 , 过点A3作y轴的垂线交l2于点A4 , …依次进行下去,则点A2017的坐标为 .
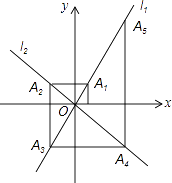
相关试题

