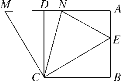
【题目】如图,在正方形ABCD中,E是AB上一点,M是AD延长线上一点,且MD=BE,连接CE,CM.
(1)求证:∠BCE=∠DCM;
(2)若点N在边AD上,且∠NCE=45°,连接NC,NE,求证:NE=BE+DN;
(3)在(2)的条件下,若DN=2,MD=3,求正方形ABCD的边长.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)正方形ABCD的边长为6.
【解析】
(1)根据正方形的性质得到CD=BC,∠ADC=∠B=90°,
根据全等三角形的性质得到∠BCE=∠DCM;
(2)根据全等三角形的性质得到∠BCE=∠DCM,CE=CM,根据全等三角形的性质得到NE=MN,等量代换即可得到结论;
(3)设正方形的边长为x根据勾股定理即可得到结论.
(1)证明:在正方形ABCD中,
∵CD=BC,∠ADC=∠B=90°,
∴∠MDC=∠B=90°,
在△BCE与△CDM中,
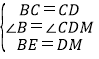 ,
,
∴△BCE≌△CDM,
∴∠BCE=∠DCM;
(2)∵∠NCE=45°,
∴∠BCE+∠DCN=45°,
∵△BCE≌△CDM,
∴∠BCE=∠DCM,CE=CM,
在△CEN与△CMN中,
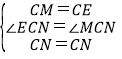 ,
,
∴△CEN≌△CMN,
∴NE=MN,
∵MN=MD+DN=BE+DN,
∴NE=BE+DN;
(3)设正方形的边长为x,
∵NE=BE+DN=MD+DN=3+2=5,AN=AD-DN=x-2,AE=x-3,
∵NE2=AN2+AE2,
∴52=(x-2)2+(x-3)2,
解得:x=6,或x=-1(不合题意,舍去),
∴正方形的边长是6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为弘扬中华传统文化,某校组织八年级1000名学生参加汉字听写大赛.为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,请根据尚未完成的下列图表,解答下列问题:
组别
分数段
频数
频率
一
50.5~60.5
16
0.08
二
60.5~70.5
30
0.15
三
70.5~80.5
m
0.25
四
80.5~90.5
80
n
五
90.5~100.5
24
0.12
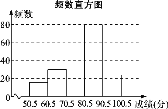
(1)写出表中:m,n,此样本中成绩的中位数落在第几组内;
(2)补全频数直方图;
(3)若成绩超过80分为优秀,该校八年级学生中汉字听写能力优秀的约有多少人?
-
科目: 来源: 题型:
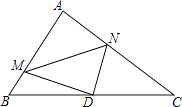
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( )
A.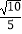
B.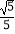
C.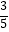
D.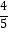
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的部分图象如图所示,则关于x的方程ax2+bx+c=0的两个根的和为 .
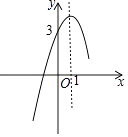
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD、BC的延长线相交于点E.

(1)求证:AD是半圆O的切线;
(2)连结CD,求证:∠A=2∠CDE. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>b,选择适当的不等号填空:
(1)-
 ________-
________- ;
;(2)1-5a__________1-5b;
(3)ax2_________bx2;
(4)a(-c2-1)_________b(-c2-1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一组数据x1,x2,…,xn的平均数为a,数据y1,y2,…,yn的平均数为b,则数据4x1+y1,4x2+y2,…,4xn+yn的平均数为__________.
相关试题

