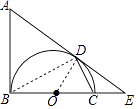
【题目】如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD、BC的延长线相交于点E. 
(1)求证:AD是半圆O的切线;
(2)连结CD,求证:∠A=2∠CDE.
参考答案:
【答案】
(1)证明:连结OD,BD,
∵AB是⊙O的切线,
∴AB⊥BC,即∠ABC=90°,
∵AB=AD,
∴∠ABD=∠ADB,
∵OB=OD,
∴∠DBO=∠BDO,
∴∠ABD+∠DBO=∠ADB+∠BDO,
∴∠ADO=∠ABO=90°,
∴AD是半圆O的切线.
(2)解:由(1)知,∠ADO=∠ABO=90°,
∴∠A=360°﹣∠ADO﹣∠ABO﹣∠BOD=180°﹣∠BOD=∠DOC,
∵AD是半圆O的切线,
∴∠ODE=90°,
∴∠ODC+∠CDE=90°,
∵BC是⊙O的直径,
∴∠ODC+∠BDO=90°,
∴∠BDO=∠CDE,
∵∠BDO=∠OBD,
∴∠DOC=2∠BDO,
∴∠DOC=2∠CDE,
∴∠A=2∠CDE.
【解析】(1)连接OD,BD,根据圆周角定理得到∠ABO=90°,根据等腰三角形的性质得到∠ABD=∠ADB,∠DBO=∠BDO,根据等式的性质得到∠ADO=∠ABO=90°,根据切线的判定定理即可得到即可;(2)由AD是半圆O的切线得到∠ODE=90°,于是得到∠ODC+∠CDE=90°,根据圆周角定理得到∠ODC+∠BDO=90°,等量代换得到∠DOC=2∠BDO,∠DOC=2∠CDE即可得到结论.
-
科目: 来源: 题型:
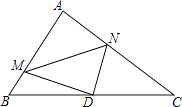
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( )
A.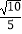
B.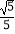
C.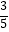
D.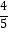
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的部分图象如图所示,则关于x的方程ax2+bx+c=0的两个根的和为 .
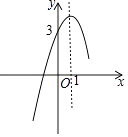
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E是AB上一点,M是AD延长线上一点,且MD=BE,连接CE,CM.
(1)求证:∠BCE=∠DCM;
(2)若点N在边AD上,且∠NCE=45°,连接NC,NE,求证:NE=BE+DN;
(3)在(2)的条件下,若DN=2,MD=3,求正方形ABCD的边长.
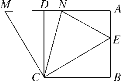
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>b,选择适当的不等号填空:
(1)-
 ________-
________- ;
;(2)1-5a__________1-5b;
(3)ax2_________bx2;
(4)a(-c2-1)_________b(-c2-1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一组数据x1,x2,…,xn的平均数为a,数据y1,y2,…,yn的平均数为b,则数据4x1+y1,4x2+y2,…,4xn+yn的平均数为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(0,4)、B(6,0)、C(0,﹣10),平移线段AB至线段CD,点Q在线段DB上,满足S△QOC:S△QOB=5:2,S△QCD=S△QBD,则点Q的坐标为_____.

相关试题

