【题目】有四根小木棒,它们的长度分别为5 cm,8 cm,12 cm,13 cm,从中选出三根作为一个三角形的三边,如果所构成的三角形为直角三角形,请回答下列问题:
(1)你所选三根木棒的长度分别为多少?请说明理由;
(2)求你所构成的直角三角形斜边上的高.
参考答案:
【答案】(1)5 cm,12 cm,13 cm;(2)![]() .
.
【解析】
根据三角形三边关系,可以判断能组成3个三角形,由于52+122=169=132,其中有一个直角三角形.
(1)所选三根木棒的长度分别为5 cm,12 cm,13 cm.理由如下:
四根木棒,任取三根,有四种组合,即5 cm,8 cm,12 cm;5 cm,12 cm,13 cm;5 cm,8 cm,13 cm;8 cm,12 cm,13 cm,
∵5+8>12,5+12>13,5+8=13(无法构成三角形),8+12>13,
∴可组成三个三角形,
又∵52=25,82=64,122=144,132=169,52+122=169=132,
∴根据勾股定理的逆定理,可知长为5 cm,12 cm,13 cm的三根木棒可构成一个直角三角形;
(2)设此直角三角形斜边上的高为x cm,
则![]() ×13x=
×13x=![]() ×5×12,即13x=60,
×5×12,即13x=60,
解得x=![]() ,
,
所以所构成的直角三角形斜边上的高是![]() cm.
cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列标志图中,既是轴对称图形,又是中心对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售甲、乙两种商品,现有如下信息:
信息1:甲、乙两种进货单价之和是3元;
信息2:甲商品零售价比进货价多1元,乙商品零售价比进货价的2倍少1元;
信息3:按零售单价购买甲商品4件和乙商品3件,共付了17元.
请根据以上信息,求甲乙两种商品的零售单价?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
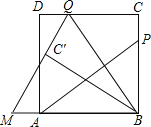
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,夜晚,小亮从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间的函数关系的图象大致为( )

A.
B.
C.
D.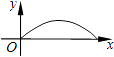
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
小明遇到这样问题:
如图1,在
 中,
中,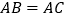 ,在AB上取一点D,在AC延长线上取一点E,若
,在AB上取一点D,在AC延长线上取一点E,若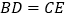 ,判断PD与PE的数量关系.
,判断PD与PE的数量关系.小明通过思考发现,可以采用两种方法解决向题:
方法一:过点D作
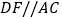 ,交BC于F,即可解决向题;
,交BC于F,即可解决向题;方法二:过点D、点E分别向直线BC引垂钱,垂足分别是F、G,也可解决问题.
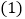 请回答:PD与PE的数量关系是______;
请回答:PD与PE的数量关系是______;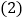 任选上述两种方法中的一种方法,在图1中补全图象,并给出证明;
任选上述两种方法中的一种方法,在图1中补全图象,并给出证明;参考小明思考问题的方法,解决问题:
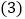 如图2,在
如图2,在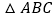 中,
中,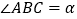 ,将AC绕点A顺时针旋转
,将AC绕点A顺时针旋转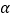 度后得到AD,过点D作
度后得到AD,过点D作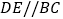 ,交AB于点E,
,交AB于点E,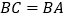 ,则图中是否存在与DE相等的线段,请找出来并给出证明.
,则图中是否存在与DE相等的线段,请找出来并给出证明.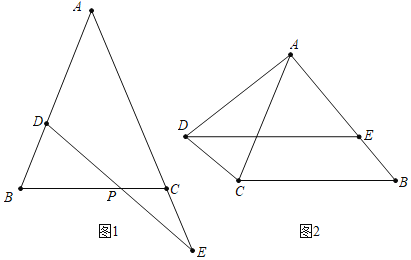
-
科目: 来源: 题型:
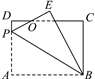
查看答案和解析>>【题目】如图,长方形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,求AP的长.
相关试题

