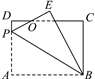
【题目】如图,长方形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,求AP的长.
参考答案:
【答案】AP=4.8.
【解析】
由折叠的性质得出EP=AP,∠E=∠A=90°,BE=AB=8,由ASA证明△ODP≌△OEG,得出OP=OG,PD=GE,设AP=EP=x,则PD=GE=6-x,DG=x,求出CG、BG,根据勾股定理得出方程,解方程即可.
如图所示,设BE与CD交于点G,

∵四边形ABCD是长方形,
∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8.,
根据题意,得△ABP≌△EBP,
∴AP=EP,∠A=∠E=90°,AB=EB=8.
在△ODP和△OEG中,
∵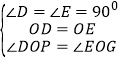 ,
,
∴△ODP≌△OEG,
∴OP=OG,PD=GE,
∴DG=EP,
设AP=EP=x,则PD=GE=6-x,DG=x,
∴CG=8-x,BG=8-(6-x)=2+x,
根据勾股定理,得BC2+CG2=BG2,
即62+(8-x)2=(2+x)2,
解得x=4.8,
∴AP=4.8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有四根小木棒,它们的长度分别为5 cm,8 cm,12 cm,13 cm,从中选出三根作为一个三角形的三边,如果所构成的三角形为直角三角形,请回答下列问题:
(1)你所选三根木棒的长度分别为多少?请说明理由;
(2)求你所构成的直角三角形斜边上的高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,夜晚,小亮从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间的函数关系的图象大致为( )

A.
B.
C.
D.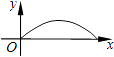
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
小明遇到这样问题:
如图1,在
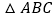 中,
中,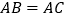 ,在AB上取一点D,在AC延长线上取一点E,若
,在AB上取一点D,在AC延长线上取一点E,若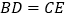 ,判断PD与PE的数量关系.
,判断PD与PE的数量关系.小明通过思考发现,可以采用两种方法解决向题:
方法一:过点D作
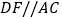 ,交BC于F,即可解决向题;
,交BC于F,即可解决向题;方法二:过点D、点E分别向直线BC引垂钱,垂足分别是F、G,也可解决问题.
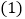 请回答:PD与PE的数量关系是______;
请回答:PD与PE的数量关系是______; 任选上述两种方法中的一种方法,在图1中补全图象,并给出证明;
任选上述两种方法中的一种方法,在图1中补全图象,并给出证明;参考小明思考问题的方法,解决问题:
 如图2,在
如图2,在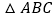 中,
中,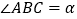 ,将AC绕点A顺时针旋转
,将AC绕点A顺时针旋转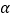 度后得到AD,过点D作
度后得到AD,过点D作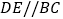 ,交AB于点E,
,交AB于点E,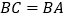 ,则图中是否存在与DE相等的线段,请找出来并给出证明.
,则图中是否存在与DE相等的线段,请找出来并给出证明.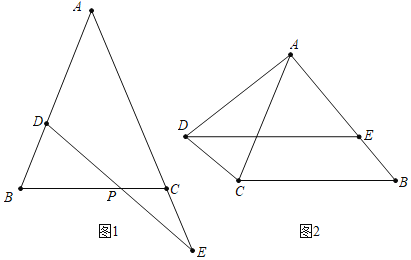
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2 , 且x1≠x2 , 则x1+x2=2,正确的个数为( )
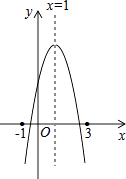
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分.某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,则与乙打平的球队是( )
A. 甲 B. 甲与丁 C. 丙 D. 丙与丁
-
科目: 来源: 题型:
查看答案和解析>>【题目】在桌面上,有若干个完全相同的小正方体堆成的一个几何体
 ,如图所示.
,如图所示.
(1)请画出这个几何体
 的三视图.
的三视图.(2)若将此几何体
 的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有_______个.
的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有_______个.(3)若现在你的手头还有一些相同的小正方体可添放在几何体
 上,要保持主视图和左视图不变,则最多可以添加________个小正方体.
上,要保持主视图和左视图不变,则最多可以添加________个小正方体.
相关试题

