【题目】(10分)如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
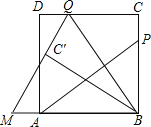
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.
参考答案:
【答案】(1)AP=BQ,理由参见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)利用BQ⊥AP和四边形ABCD是正方形的条件证明△PBA≌△QCB即可;(2)过点Q作QH⊥AB于H,可得QH=BC=AB=3,∵BP=2PC,∴BP=2,PC=1,运用勾股定理可求得AP(即BQ)=![]() ,BH=2.由DC∥AB,得∠CQB=∠QBA.由折叠角相等可得∠C′QB=∠CQB,等量代换:∠QBA=∠C′QB,根据等角对等边得:MQ=MB.设QM=x,则有MB=x,MH=x﹣2.在Rt△MHQ中运用勾股定理求得QM;(3)过点Q作QH⊥AB于H,用(2)的思路方法求出QM的长,也就知道BM的长了,再减去AB的长就是AM的长.
,BH=2.由DC∥AB,得∠CQB=∠QBA.由折叠角相等可得∠C′QB=∠CQB,等量代换:∠QBA=∠C′QB,根据等角对等边得:MQ=MB.设QM=x,则有MB=x,MH=x﹣2.在Rt△MHQ中运用勾股定理求得QM;(3)过点Q作QH⊥AB于H,用(2)的思路方法求出QM的长,也就知道BM的长了,再减去AB的长就是AM的长.
试题解析:(1)证明线段相等,通常证明所在的三角形全等,此题利用BQ⊥AP和四边形ABCD是正方形的条件证明△PBA≌△QCB,证明:∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠C=90°,∴∠ABQ+∠CBQ=90°.∵BQ⊥AP,∴∠PAB+∠QBA=90°,∴∠PAB=∠CBQ(同角的余角相等).∴△PBA≌△QCB(ASA),∴AP=BQ(全等三角形的对应边相等);(2)过点Q作QH⊥AB于H,如图:∵四边形ABCD是正方形,∴QH=BC=AB=3.∵BP=2PC,BP+PC=3,∴BP=2,PC=1,∵△PBA≌△QCB,∴CQ=BP=2,四边形QHCB是矩形,∴BH=CQ=2,∵四边形ABCD是正方形,∴DC∥AB,∴∠CQB=∠QBA.由折叠角相等可得∠C′QB=∠CQB,∴∠QBA=∠C′QB(等量代换),∴MQ=MB(等角对等边).设QM=x,则有MB=x,MH=x﹣2.在Rt△MHQ中,根据勾股定理可得x2=(x﹣2)2+32,解得x=![]() .∴QM的长为
.∴QM的长为![]() ;
;
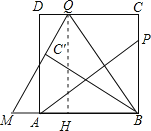
过点Q作QH⊥AB于H,如上题的思路可得:四边形ABCD是正方形,BP=m,PC=n,∴QH=BC=AB=m+n.∵△PBA≌△QCB,∴CQ=BP=m,四边形QHCB是矩形,∴BH=CQ=m.设QM=x,则有MB=QM=x,MH=x﹣m.在Rt△MHQ中,根据勾股定理可得x2=(x﹣m)2+(m+n)2,解得x=m+n+![]() ,∴AM=MB﹣AB=m+n+
,∴AM=MB﹣AB=m+n+![]() ﹣m﹣n=
﹣m﹣n=![]() .即AM的长为
.即AM的长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列关系错误的是( )

A. ∠AOC=∠AOB+∠BOC
B. ∠AOC=∠AOD-∠COD
C. ∠AOC=∠AOB+∠BOD-∠BOC
D. ∠AOC=∠AOD-∠BOD+∠BOC
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列标志图中,既是轴对称图形,又是中心对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售甲、乙两种商品,现有如下信息:
信息1:甲、乙两种进货单价之和是3元;
信息2:甲商品零售价比进货价多1元,乙商品零售价比进货价的2倍少1元;
信息3:按零售单价购买甲商品4件和乙商品3件,共付了17元.
请根据以上信息,求甲乙两种商品的零售单价?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有四根小木棒,它们的长度分别为5 cm,8 cm,12 cm,13 cm,从中选出三根作为一个三角形的三边,如果所构成的三角形为直角三角形,请回答下列问题:
(1)你所选三根木棒的长度分别为多少?请说明理由;
(2)求你所构成的直角三角形斜边上的高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,夜晚,小亮从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间的函数关系的图象大致为( )

A.
B.
C.
D.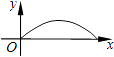
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
小明遇到这样问题:
如图1,在
 中,
中,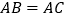 ,在AB上取一点D,在AC延长线上取一点E,若
,在AB上取一点D,在AC延长线上取一点E,若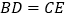 ,判断PD与PE的数量关系.
,判断PD与PE的数量关系.小明通过思考发现,可以采用两种方法解决向题:
方法一:过点D作
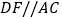 ,交BC于F,即可解决向题;
,交BC于F,即可解决向题;方法二:过点D、点E分别向直线BC引垂钱,垂足分别是F、G,也可解决问题.
 请回答:PD与PE的数量关系是______;
请回答:PD与PE的数量关系是______;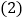 任选上述两种方法中的一种方法,在图1中补全图象,并给出证明;
任选上述两种方法中的一种方法,在图1中补全图象,并给出证明;参考小明思考问题的方法,解决问题:
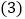 如图2,在
如图2,在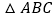 中,
中,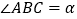 ,将AC绕点A顺时针旋转
,将AC绕点A顺时针旋转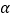 度后得到AD,过点D作
度后得到AD,过点D作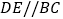 ,交AB于点E,
,交AB于点E,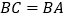 ,则图中是否存在与DE相等的线段,请找出来并给出证明.
,则图中是否存在与DE相等的线段,请找出来并给出证明.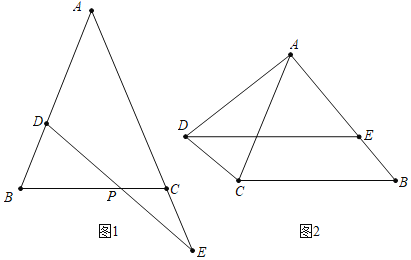
相关试题

