【题目】如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( ) 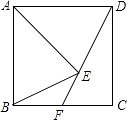
A.35°
B.45°
C.55°
D.60°
参考答案:
【答案】B
【解析】解:∵四边形ABCD是正方形, ∴AB=AD,∠BAD=90°,
∵AE=AB,
∴AE=AB=AD,
∴∠ABE=∠AEB,∠AED=∠ADE,∠ABE+∠AEB+∠BAE=180°,∠AED+∠ADE+∠DAE=180°,
∵∠BAE+∠DAE=∠BAD=90°,
∴∠ABE+∠AEB+∠AED+∠ADE=270°,
∴∠AEB+∠AED=135°,
即∠BED=135°,
∴∠BEF=180°﹣135°=45°.
故选:B.
【考点精析】本题主要考查了等腰三角形的性质和正方形的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=90°,
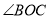 是锐角,ON平分
是锐角,ON平分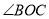 ,OM平分∠AOB.
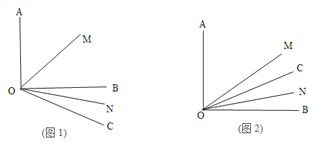
,OM平分∠AOB.(1)如图1若
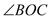 =30°,求
=30°,求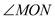 的度数?
的度数?(2)若射线OC绕着点O运动到∠AOB的内部(如图2),在(1)的条件下求
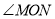 的度数;
的度数;(3)若∠AOB=
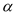 (90°≤
(90°≤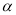 <180°),
<180°),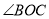 =
= 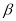 (0°<
(0°<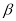 <90°),请用含有
<90°),请用含有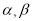 的式子直接表示上述两种情况
的式子直接表示上述两种情况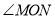 的度数.
的度数.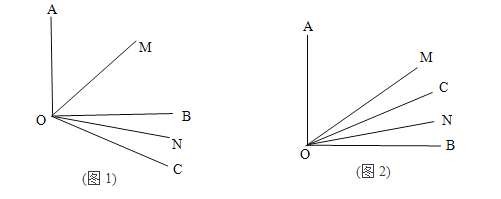
【答案】(1)60°;(2)30°;(3)①∠MON=
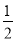 (
(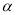 +
+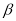 ),;②∠MON=
),;②∠MON=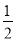 (
(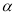 -
- ).
).【解析】试题分析:(1)由于∠AOB=90°,∠BOC=30°,OM平分∠AOB,ON平分∠BOC,所以可以求得∠MOB和∠NOB的度数,进而求得∠MON的度数;(2)类比(1)的方法求解即可;(3)结合(1)(2)题的计算方法求解即可.
试题解析:
(1)∵OM平分∠AOB,ON平分∠BOC,
∴∠BOM=
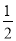 ∠AOB,∠BON=
∠AOB,∠BON= ∠BOC.
∠BOC.∵∠AOB=90°,∠BOC=30°,
∴∠BOM=
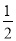 ×90°=45°,∠BON=
×90°=45°,∠BON=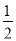 ×30°=15°,
×30°=15°,∴∠MON=∠BOM+∠BON=45°+15°=60°.
(2)由(1)可知:∠BOM=45°,∠BON=15°,
∴∠MON=∠BOM-∠BON=45°-15°=30°.
(3)①∠MON=
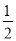 (
(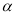 +
+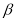 ),②∠MON=
),②∠MON=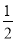 (
(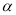 -
-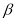 ).
).点睛:本题主要考查学生角平分线的定义及角的计算的理解和掌握,在解决角与角之间的关系时,要充分利用已知条件和图中的隐含条件.
【题型】解答题
【结束】
27【题目】(1)已知线段AB=8cm,在线段AB上有一点C,且BC=4cm,M为线段AC的中点.
①求线段AM的长?
②若点C在线段AB的延长线上,AM的长度又是多少呢?
(2)如图,AD=
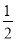 DB,E是BC的中点,BE=
DB,E是BC的中点,BE=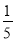 AC=2cm,求DE的长.
AC=2cm,求DE的长.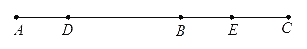
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=2x-5的图象不经过的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2﹣9= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线F与x轴相交于A、B两点(点A在点B的左边),对称轴为直线x=1,顶点C在直线
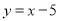 上,与y轴相交于点D(0,3)。
上,与y轴相交于点D(0,3)。(1)求抛物线F的解析式;
(2)连结CD、BD,则线段BD与CD的数量关系和位置关系分别为 ;
(3)点P为直线CD上方抛物线F上的一个动点,PQ⊥CD,垂足为Q,若∠QPD=∠DBC,求点P的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题中①平行于同一条直线的两条直线平行;②垂直于同一条直线的两条直线平行;③过一点有且只有一条直线与已知直线平行;④过一点有且只有一条直线与已知直线垂直.为真命题的是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班体育课上,老师测试10个同学做引体向上的成绩,10个同学的成绩记录见下表:
引体向上的个数
5
6
7
人数
3
4
3
则这10个同学做引体向上的成绩的平均数是( )
A. 4 B. 5 C. 6 D. 7
相关试题

