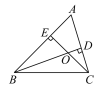
【题目】如图,在△ABC中,BD是AC边上的高,CE是AB边上的高,BD与CE相交于点O,则∠ABD___∠ACE(填“>”“<”或“=”),∠A+∠DOE=___度.
参考答案:
【答案】=180
【解析】
根据三角形内角和等于180°,四边形内角和等于360°可求解.
∵BD是AC边上的高,CE是AB边上的高,
∴∠AEC=∠ADB=90°
∵∠ABD+∠A+∠ADB=180°,∠ACE+∠A+∠AEC=180°,
∴∠ABD=180°-∠A-∠ADB,∠ACE=180°-∠A-∠AEC,
∴∠ABD=∠ACE,
在四边形AEOD中,∵∠A+∠AEO+∠EOD+∠ODA=360°,
∵∠AEC=∠ADB=90°,
∴∠A+∠EOD=360°-∠AEO-∠ODA=360°-90°-90°=180°.
故答案为:=;180.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折得到△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )

A. 115° B. 105° C. 95° D. 85°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数是( )

A. 400 B. 450 C. 500 D. 600
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣2x+10与x轴,y轴相交于A,B两点,点C的坐标是(8,4),连接AC,BC.
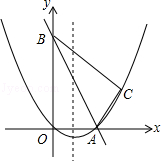
(1)求过O,A,C三点的抛物线的解析式,并判断△ABC的形状;
(2)动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t秒,当t为何值时,PA=QA?
(3)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
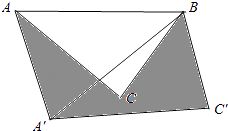
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=45°,AB=4cm,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为cm2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线
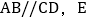 为直线AB、CD之间的一点.
为直线AB、CD之间的一点.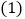 如图1,若
如图1,若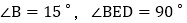 ,则
,则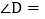 ______ ;
______ ;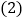 如图2,若
如图2,若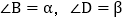 ,则
,则 ______ ;
______ ;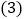 如图3,若
如图3,若 ,则
,则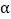 、
、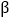 与
与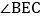 之间有什么等量关系?请猜想证明.
之间有什么等量关系?请猜想证明.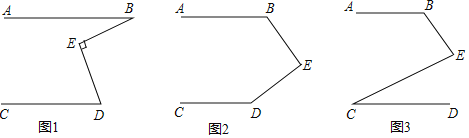
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的外心为O,内心为I,∠BOC=120°,∠BIC= .
相关试题

