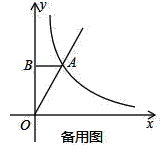
【题目】如图,在平面直角坐标系中,直线y=kx和双曲线![]() 在第一象限相交于点A(1,2),点B在y轴上,且AB⊥y轴.有一动点P从原点出发沿y轴以每秒1个单位的速度向y轴的正方向运动,运动时间为t秒(t>0),过点P作PD⊥y轴,交直线OA于点C,交双曲线于点D.
在第一象限相交于点A(1,2),点B在y轴上,且AB⊥y轴.有一动点P从原点出发沿y轴以每秒1个单位的速度向y轴的正方向运动,运动时间为t秒(t>0),过点P作PD⊥y轴,交直线OA于点C,交双曲线于点D.
(1)求直线y=kx和双曲线![]() 的函数关系式;
的函数关系式;
(2)设四边形CDAB的面积为S,当P在线段OB上运动时(P不与B点重合),求S与t之间的函数关系式;
(3)在图中第一象限的双曲线上是否存在点Q,使以A、B、C、Q四点为顶点的四边形是平行四边形?若存在,请求出此时t的值和Q点的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 时,Q
时,Q![]() ;
;![]() 时,Q
时,Q![]() ;
;![]() 时,
时,![]() ;
;
【解析】
(1)把点A的坐标代入两个函数的解析式求出k和k′的值即可得到两个函数的解析式;
(2)由题意易得AB=1,OB=2,OP=t,结合(1)中所得两个函数的解析式可得:PC=![]() ,PD=
,PD=![]() ,BP=
,BP=![]() ,由此可得当点P在线段AB上(不与点B重合)时,CD=PD-PC=
,由此可得当点P在线段AB上(不与点B重合)时,CD=PD-PC=![]() ,这样S=S梯形ABCD=
,这样S=S梯形ABCD=![]() (AB+CD)·BP即可求得S与t间的函数关系式了;
(AB+CD)·BP即可求得S与t间的函数关系式了;
(3)根据题意,分①CD在AB的下方,AB∥CD,且AB=CD,点Q与点D重合;②CD在AB上方,AB∥CD,且AB=CD,点Q与点D重合;③CD在AB下方,BQ∥AC,BQ=AC;根据这三种情况画出对应的图形(图2和图3)结合已知条件进行分析解答即可.
(1)把A(1,2)代入y=kx和y=![]() ,
,
k=2,k′=2
∴直线y=kx的函数关系式是y=2x,双曲线y=![]() 的函数关系式是y=
的函数关系式是y=![]() ;
;
(2)由题意可得:AB=1,OB=2,OP=t,
∴PC=![]() ,PD=
,PD=![]() ,BP=2-t,
,BP=2-t,
∴当CD在AB下方时,CD=PD-PC=![]() -
-![]() .
.
∴S=![]() (1+
(1+![]() -
-![]() )(2-t)=
)(2-t)= ![]() (0<t<2);
(0<t<2);
(3)存在以下3种情形,具体如下:
①当CD在AB的下方,AB∥CD,且AB=CD,点Q与点D重合(如图2)时,四边形ABCQ是平行四边形,
∵CD=PD-PC=![]() -
-![]() =1,
=1,
∴![]() ,解得
,解得![]() (舍去),
(舍去),
∴此时PD=![]() =
=![]() ,OP=t=
,OP=t=![]() -1,
-1,
∴当t=![]() -1时,存在Q(
-1时,存在Q(![]() ,
,![]() -1)使以A、B、C、Q四点为顶点的四边形是平行四边形;
-1)使以A、B、C、Q四点为顶点的四边形是平行四边形;
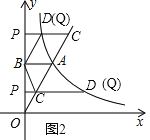
②当CD在AB的上方,AB∥CD,且AB=CD,点Q与点D重合(如图2)时,四边形ACBQ是平行四边形,
∵CD=PC-PD,
∴![]() ,解得:
,解得:![]() (舍去),
(舍去),
∴此时PD=![]() =
=![]() ,OP=t=
,OP=t=![]() +1,
+1,
∴当t=![]() +1时,存在Q(
+1时,存在Q(![]() ,
,![]() +1)使以A、B、C、Q四点为顶点的四边形是平行四边形;
+1)使以A、B、C、Q四点为顶点的四边形是平行四边形;
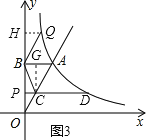
③当BQ∥AC,BQ=AC,且CD在AB下方时(如图3),此时四边形ACBQ是平行四边形,
此时Q点的坐标仍为(![]() ,
,![]() +1),
+1),
过C作CG⊥AB交AB于G,过Q作QH⊥y轴交y轴于H,
易证:△ACG≌△QBH,
∴CG=BH=BP,,
∴OP=2OB-OH=4-(![]() +1)=3-
+1)=3-![]() ,
,
∴当t=3-![]() 时,存在Q(
时,存在Q(![]() ,
,![]() +1)使以A、B、C、Q四点为顶点的四边形是平行四边形.
+1)使以A、B、C、Q四点为顶点的四边形是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中,正确的是( )
A.a0=1
B.a﹣1=﹣a
C.a3a2=a5
D.2a2+3a3=5a5 -
科目: 来源: 题型:
查看答案和解析>>【题目】在求1+3+32+33+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38①, 然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39②,
②﹣①得,3S﹣S=39﹣1,即2S=39﹣1,
所以S= .
.
得出答案后,爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正确答案是 . -
科目: 来源: 题型:
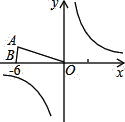
查看答案和解析>>【题目】已知:等腰△OAB在直角坐标系中的位置如图,点A坐标为
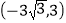 ,点B坐标为(-6,0).
,点B坐标为(-6,0).(1)若将△OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数
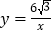 的图象上,求a的值;
的图象上,求a的值;(2)若△OAB绕点O按逆时针方向旋转α度(0<α<360).
①当α=30°时,点B恰好落在反比例函数
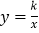 的图象上,求k的值;
的图象上,求k的值;②问点A、B能否同时落在①中的反比例函数的图象上?若能,直接写出α的值;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.

(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算: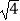 +20170﹣|
+20170﹣| 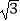 ﹣2|+1
﹣2|+1
(2)计算: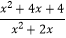 ÷(2x﹣
÷(2x﹣ 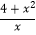 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点M,O,N对应的数分别为﹣3,0,1,点P为数轴上任意一点,其对应的数为x.
(1)如果点P到点M、点N的距离相等,那么x的值是 ;
(2)当x= 时,使点P到点M、点N的距离之和是5;
(3)如果点P以每秒钟3个单位长度的速度从点O向左运动时,点M和点N分别以每秒钟1个单位长度和每秒钟4个单位长度的速度也向左运动,且三点同时出发,那么 秒钟时点P到点M,点N的距离相等.
相关试题

