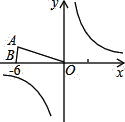
【题目】已知:等腰△OAB在直角坐标系中的位置如图,点A坐标为![]() ,点B坐标为(-6,0).
,点B坐标为(-6,0).
(1)若将△OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数![]() 的图象上,求a的值;
的图象上,求a的值;
(2)若△OAB绕点O按逆时针方向旋转α度(0<α<360).
①当α=30°时,点B恰好落在反比例函数![]() 的图象上,求k的值;
的图象上,求k的值;
②问点A、B能否同时落在①中的反比例函数的图象上?若能,直接写出α的值;若不能,请说明理由.
参考答案:
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() =60°
=60°
【解析】
(1)由题意可得将△AOB向右平移a个单位后点A 坐标为![]() ,将此时点A的坐标代入
,将此时点A的坐标代入![]() 中,即可求得a的值;
中,即可求得a的值;
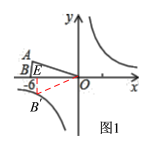
(2)①如图1,设旋转后点B的对应点是点B′,连接OB′,过点B′作B′E⊥x轴于点E,则由题意可得OB′=OB=6,∠EOB′=30°,由此在△OB′E中求得B′E和OE的长,即可得到此时点B′的坐标,将点B′的坐标代入![]() 中即可求得k的值;
中即可求得k的值;
②如图2,当点A旋转后落到①中B′的位置上,同时点B旋转到了B′′的位置上,过点B′′作B′′F⊥y轴于点F,结合已知条件求出此时点B′′的坐标,得到此时点B′′也在①中反比例函数的图象上的结论,再求得∠AOB的度数,即可得到此时的旋转角![]() 的值了.
的值了.
(1)由题意可知,将△AOB向右平移a个单位后点A 坐标为![]() ,
,
∵平移后的点A刚好落在反比例函数![]() 的图象上,
的图象上,
∴![]() ,解得:
,解得:![]() ;
;
(2)①如图1,设旋转后点B的对应点是点B′,连接OB′,过点B′作B′E⊥x轴于点E,则由题意可得OB′=OB=6,∠EOB′=30°,
∴∠OEB′=90°,
∴OE=OB′·cos30°=![]() ,B′E=OB′·sin30°=
,B′E=OB′·sin30°=![]() ,
,
∴点B′的坐标为![]() ,
,
∵此时点B′在反比例函数![]() 的图象上,
的图象上,
∴![]() ;
;
②能,理由如下:
∵点A的坐标为![]() ,
,
∴tan∠AOB=![]() ,
,
∴∠AOB=30°,
∵OA=OB=6,
∴当旋转后点A落在①中B′的位置时,此时点A′在①中的反比例函数的图象上(如图2),此时点B旋转到了B′′的位置上,则∠A′OB=30°,
∴此时∠AOA′=60°,
∴∠BOB′′=60°,
∴∠B′′OF=30°,
过点B′′作B′′F⊥y轴于点F,则∠B′′FO=90°,
∴OF=OB′′·cos30°=![]() ,B′′F=OB′′·sin30°=
,B′′F=OB′′·sin30°=![]() ,
,
∴此时点B′′的坐标为![]() ,
,
∵![]() ,
,
∴此时点B′′在①中反比例函数的图象上,
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)某校有学生2000名,为了了解学生在篮球、足球、排球和乒乓球这四项球类运动中最喜爱的一项球类运动情况,对学生开展了随机调查,丙将结果绘制成如下的统计图.

请根据以上信息,完成下列问题:
(1)本次调查的样本容量是 ;
(2)某位同学被抽中的概率是 ;
(3)据此估计全校最喜爱篮球运动的学生人数约有 名;
(4)将条形统计图补充完整.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中,正确的是( )
A.a0=1
B.a﹣1=﹣a
C.a3a2=a5
D.2a2+3a3=5a5 -
科目: 来源: 题型:
查看答案和解析>>【题目】在求1+3+32+33+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38①, 然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39②,
②﹣①得,3S﹣S=39﹣1,即2S=39﹣1,
所以S= .
.
得出答案后,爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正确答案是 . -
科目: 来源: 题型:
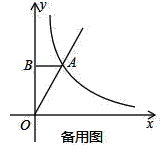
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=kx和双曲线
 在第一象限相交于点A(1,2),点B在y轴上,且AB⊥y轴.有一动点P从原点出发沿y轴以每秒1个单位的速度向y轴的正方向运动,运动时间为t秒(t>0),过点P作PD⊥y轴,交直线OA于点C,交双曲线于点D.
在第一象限相交于点A(1,2),点B在y轴上,且AB⊥y轴.有一动点P从原点出发沿y轴以每秒1个单位的速度向y轴的正方向运动,运动时间为t秒(t>0),过点P作PD⊥y轴,交直线OA于点C,交双曲线于点D.(1)求直线y=kx和双曲线
 的函数关系式;
的函数关系式;(2)设四边形CDAB的面积为S,当P在线段OB上运动时(P不与B点重合),求S与t之间的函数关系式;
(3)在图中第一象限的双曲线上是否存在点Q,使以A、B、C、Q四点为顶点的四边形是平行四边形?若存在,请求出此时t的值和Q点的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.

(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算: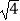 +20170﹣|
+20170﹣| 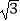 ﹣2|+1
﹣2|+1
(2)计算: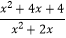 ÷(2x﹣
÷(2x﹣ 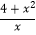 )
)
相关试题

