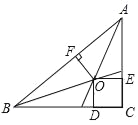
【题目】如图,在△ABC中,∠C=90°,O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且BC=8cm,CA=6cm,则点O到边AB的距离为( )
A. 2cm B. 3cm C. 4cm D. 5cm
参考答案:
【答案】A
【解析】
根据角平分线的性质得到OE=OF=OD,设OE=x,然后利用三角形面积公式得到S△ABC=S△OAB+S△OAC+S△OCB,于是可得到关于x的方程,从而可得到OF的长度.
在△ABC中,∵∠C=90°,BC=8cm,CA=6cm,∴AB=10cm.
∵点O为△ABC的三条角平分线的交点,∴OE=OF=OD,设OE=x.
∵S△ABC=S△OAB+S△OAC+S△OCB,∴![]() ×6×8=
×6×8=![]() OF×10+
OF×10+![]() OE×6+
OE×6+![]() OD×8,∴5x+3x+4x=24,∴x=2,∴点O到AB的距离等于2.
OD×8,∴5x+3x+4x=24,∴x=2,∴点O到AB的距离等于2.
故选A.
-
科目: 来源: 题型:
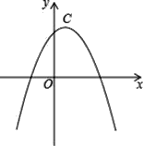
查看答案和解析>>【题目】若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线C1:y1=﹣2x2+4x+2与C2:u2=﹣x2+mx+n为“友好抛物线”.
(1)求抛物线C2的解析式.
(2)点A是抛物线C2上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.
(3)设抛物线C2的顶点为C,点B的坐标为(﹣1,4),问在C2的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线C2上?若存在求出点M的坐标,不存在说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解同学们每月零花钱数额,校园小记者随机调查了本校部分学生,并根据调查结果绘制出如下不完整的统计图表:
零花钱数额
 元
元人数(频数)
频率

6
0.15

12
0.30

16
0.40


0.10

2


请根据以下图表,解答下列问题:
(1)这次被调查的人数共有__________人,
 __________;
__________;(2)计算并补全频数分布直方图;
(3)请估计该校1500名学生中每月零花钱数额低于90的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请从以下四个一元二次方程中任选三个,并用适当的方法解这三个方程.
(1)x2﹣x﹣1=0;
(2)(y﹣2)2﹣12=0;
(3)(1+m)2=m+1;
(4)t2﹣4t=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△EAD;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CEF其中正确的是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)如图,在四边形ABCD中,AD∥BC,点E在BC的延长线上,CE=BC,连接AE,交CD边于点F,且CF=DF.(1)求证:AD=BC;(2)连接BD、DE,若BD⊥DE,求证:四边形ABCD为菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C、P四点均在边长为1的小正方形网格格点上.
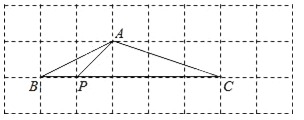
(1)判断△PBA与△ABC是否相似,并说明理由;
(2)求∠BAC的度数.
相关试题

