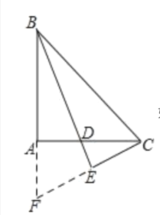
【题目】如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD交BD的延长线于点E,若BD=2,则CE=_________.

参考答案:
【答案】1
【解析】
延长BA、CE相交于点F,利用“角边角”证明△BCE和△BFE全等,根据全等三角形对应边相等可得CE=EF,根据等角的余角相等求出∠ABD=∠ACF,然后利用“角边角”证明△ABD和△ACF全等,根据全等三角形对应边相等可得BD=CF,然后求解即可.
如图,延长BA、CE相交于点F,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△BCE和△BFE中,
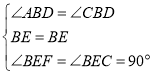 ,
,
∴△BCE≌△BFE(ASA),
∴CE=EF,
∵∠BAC=90°,CE⊥BD,
∴∠ACF+∠F=90°,∠ABD+∠F=90,
∴∠ABD=∠ACF,
在△ABD和△ACF中,
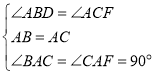 ,
,
∴△ABD≌△ACF(ASA),
∴BD=CF,
∵CF=CE+EF=2CE,
∴BD=2CE=2,
∴CE=1.
故答案为:1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200立方米的生活垃圾运走.
(1)假如每天能运x立方米,所需时间为y天,写出y与x之间的函数解析式(不要求写出自变量的取值范围);
(2)若每辆拖拉机一天能运12立方米,则5辆这样的拖拉机要用多少天才能运完?
(3)在(2)的条件下,运了8天后,剩下的任务要在不超过6天的时间内完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,下列说法:①∠APE=∠C,②AQ=BQ,③BP=2PQ,④AE+BD=AB,其中正确的个数有( )个。
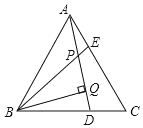
A. 4B. 3C. 2D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个主持人站在舞台的黄金分割点处最自然得体,如果舞台AB长为20米,一个主持人现在站在A处,那么他应至少再走________米才最理想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平面直角坐标系中,点A的坐标为(m,0),点B的坐标为(0,n),其中m=
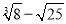 ,
,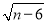 =0,将三角形BOA沿x轴的正方向向右平移10个单位长度得到三角形CDE,连接BC.
=0,将三角形BOA沿x轴的正方向向右平移10个单位长度得到三角形CDE,连接BC.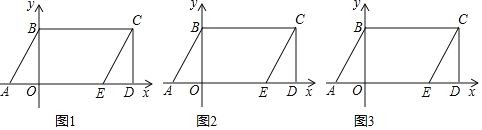
(1)如图1,分别求点C、点E的坐标;
(2)点P自点C出发,以每秒1个单位长度沿线段CB运动,同时点Q自点O出发,以每秒2个单位长度沿线段OE运动,连接AP、BQ,点Q运动至点E时,点P同时停止运动.设运动时间t(秒),三角形ABQ的面积与三角形APB的面积的和为s(平方单位),求s与t的关系式,并直接写出t的取值范围;
(3)在(2)的条件下,BP:QE=8:3,此时将线段PQ向左平移2个单位长度得到线段P'Q'(点P'与点P对应),线段P′Q'再向下平移2个单位长度得到线段MN(点M与点P'对应),线段MN交x轴于点G,点H在线段OA上,OH=
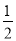 OG,过点H作HR⊥OA,交AB于点R,求点R的坐标.
OG,过点H作HR⊥OA,交AB于点R,求点R的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】小刚准备用一段长 44 米的篱笆围成三角形,用于养鸡。已知一条边长 x 米,第二条边是第一条边的 3 倍多 6 米。
(1)若能围成一个等腰三角形,求三边长
(2)若第一边长最短,写出 x 的取值范围 。
-
科目: 来源: 题型:
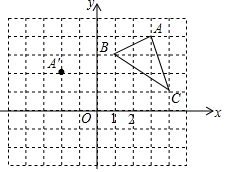
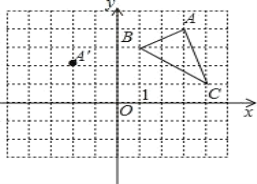
查看答案和解析>>【题目】在平面直角坐标系中,△ABC 的三个顶点的位置如图所示,点 A′的坐标是(-2,2),现将△ABC 平移,使点 A 变换为点 A′,点 B′、C′分别是 B、C 的对应点.
(1) 请画出平移后的△A′B′C′(不写画法),并直接写出点B′、C′的坐标:B′ 、C′ ;
(2) 若△ABC 内部一点 P 的坐标为(
 ,
,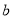 ),则点 P 的对应点 P′的坐标是 ;
),则点 P 的对应点 P′的坐标是 ;(3) 连接 A′B,CC′,并求四边形 A′BCC′的面积.
相关试题

