【题目】某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200立方米的生活垃圾运走.
(1)假如每天能运x立方米,所需时间为y天,写出y与x之间的函数解析式(不要求写出自变量的取值范围);
(2)若每辆拖拉机一天能运12立方米,则5辆这样的拖拉机要用多少天才能运完?
(3)在(2)的条件下,运了8天后,剩下的任务要在不超过6天的时间内完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
参考答案:
【答案】(1)![]() ;(2)20;(3)5
;(2)20;(3)5
【解析】(1)根据每天能运xm3,所需时间为y天的积就是1200m3,即可写出函数关系式;
(2)把x=12×5=60代入,即可求得天数;
(3)首先算出8天以后剩余的数量,然后计算出6天运完所需的拖拉机数,即可求解.
(1)∵xy=1200,∴y=![]() ;
;
(2)x=12×5=60,将x=60代入y=![]() ,
,
得y=![]() =20,
=20,
答:5辆这样的拖拉机要用20天才能运完;
(3)运了8天后剩余的垃圾有1200-8×60=720(米3),
剩下的任务要在不超过6天的时间内完成,则每天至少运720÷6=120(米3),则需要拖拉机120÷12=10(辆),10-5=5(辆),
即至少需要增加5辆这样的拖拉机才能按时完成任务.
-
科目: 来源: 题型:
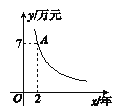
查看答案和解析>>【题目】朱先生利用分期付款的形式购买了一套住房,他购买的住房的价格为24万元,交了首付之后每年付款y万元,x年结清余款,y与x的函数关系如图所示,请根据图象所提供的信息,回答下列问题:
(1)确定y与x的函数解析式,并求出首付款的数目;
(2)朱先生若用10年结清余款,则每年应付多少钱?
(3)如果朱先生打算每年付款不超过7000元,那么他至少需要几年才能结清余款?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:直线AB与直线PQ交于点E,直线CD与直线PQ交于点F,∠PEB+∠QFD=180°.
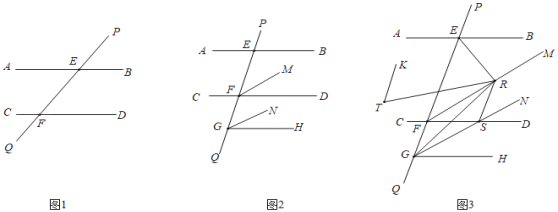
(1)如图1,求证:AB∥CD;
(2)如图2,点G为直线PQ上一点,过点G作射线GH∥AB,在∠EFD内过点F作射线FM,∠FGH内过点G作射线GN,∠MFD=∠NGH,求证:FM∥GN;
(3)如图3,在(2)的条件下,点R为射线FM上一点,点S为射线GN上一点,分别连接RG、RS、RE,射线RT平分∠ERS,∠SGR=∠SRG,TK∥RG,若∠KTR+∠ERF=108°,∠ERT=2∠TRF,∠BER=40°,求∠NGH的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按图中所标注的数据,计算图中实线所围成的面积S是( )

A.50B.62C.65D.68
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,下列说法:①∠APE=∠C,②AQ=BQ,③BP=2PQ,④AE+BD=AB,其中正确的个数有( )个。
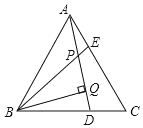
A. 4B. 3C. 2D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个主持人站在舞台的黄金分割点处最自然得体,如果舞台AB长为20米,一个主持人现在站在A处,那么他应至少再走________米才最理想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD交BD的延长线于点E,若BD=2,则CE=_________.

相关试题

