【题目】如图,已知射线CB//OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
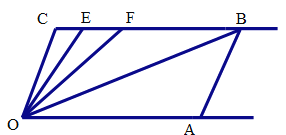
(1)求∠EOB的度数.(直接写出结果,无需解答过程)
∠EOB=__________°
(2)若在OC右侧左右平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,请找出变化规律;若不变,请求出这个比值.
(3)在OC右侧左右平行移动AB的过程中,是否存在使∠OEC=∠OBA的情况?若存在,请直接写出∠OEC度数;若不存在,请说明理由.
参考答案:
【答案】(1)40°;(2)不变;(3)存在,∠OEC=60°
【解析】
(1)根据平行线的性质以及角平分线的性质即可得出答案,
(2)根据平行线的性质可得出∠OBC=∠BOA,∠OFC=∠FOA,从而得出答案,
(3)根据平行四边形的性质即可得出答案.
解:(1)∵CB∥OA,∠C=∠OAB=100°,
∴∠COA=180°-∠C=180°-100°=80°,
∵CB∥OA,
∴∠FBO=∠AOB,
又∵∠FOB=∠AOB,
∴∠FBO=∠FOB,
∴OB平分∠AOF,
又∵OE平分∠COF,
∴∠EOB=∠EOF+∠FOB=![]() ∠COA=
∠COA=![]() ×80°=40°;
×80°=40°;
故填:40°
(2)不变,
∵CB∥OA,则∠OBC=∠BOA,∠OFC=∠FOA,
则∠OBC:∠OFC=∠AOB:∠FOA,
又∵∠FOA=∠FOB+∠AOB=2∠AOB,
∴∠OBC:∠OFC=∠AOB:∠FOA=∠AOB:2∠AOB=1:2,
(3)∵CB∥OA,∠C=∠OAB=100°,
∴∠AOC=∠ABC=80°,
则四边形AOCB为平行四边形,
则∠OEC=∠EOB+∠OBF=∠EOB+∠AOB,
∠OBA=∠BOC=∠COE+∠EOB,
又∵∠OEC=∠OBA,
则∠AOB=∠COE,
则∠COE=∠EOF=∠FOB=∠AOB=80°÷4=20°,
则∠EOB=2×20°=40°,
此时∠OEC=40°+20°=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,对角线AC与BD交于点O,若增加一个条件,使ABCD成为菱形,下列给出的条件不正确的是( )

A.AB=AD
B.AC⊥BD
C.AC=BD
D.∠BAC=∠DAC -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点
 为第一象限内一点,点
为第一象限内一点,点 为
为 轴正半轴上一点,分别连接
轴正半轴上一点,分别连接 ,
, ,
, 为等边三角形,点
为等边三角形,点 的横坐标为4.
的横坐标为4.
(1)如图1,求线段
 的长;
的长;(2)如图2,点
 在线段
在线段 上(点
上(点 不与点
不与点 、点
、点 重合),点
重合),点 在线段
在线段 的延长线上,连接
的延长线上,连接 ,
, ,
, ,设
,设 的长为
的长为 ,
, 的长为
的长为 ,求
,求 与
与 的关系式(不要求写出
的关系式(不要求写出 的取值范围)
的取值范围)(3)在(2)的条件下,点
 为第四象限内一点,分别连接
为第四象限内一点,分别连接 ,
,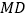 ,
, ,
, 为等边三角形,线段
为等边三角形,线段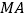 的垂直平分线交
的垂直平分线交 的延长线于点
的延长线于点 ,交
,交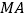 于点
于点 ,连接
,连接 ,交
,交 于点
于点 ,连接
,连接 ,若
,若 ,求点
,求点 的横坐标.
的横坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若AB∥CD,EF与AB 、CD分别相交于E、F,EP⊥EF,∠EFD的平分线与EP相交于点P,且∠BEP=40°,求∠EFP的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:如图①,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
特例探究:如图②,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC, CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;
归纳证明:如图③,点BC在∠MAN的边AM、AN上,点EF在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC, ∠1=∠2=∠BAC.求证:△ABE≌△CAF;
拓展应用:如图④,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为 .(12分)




-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
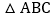 中,
中,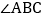 和
和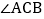 的平分线相交于点O,过O点作
的平分线相交于点O,过O点作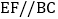 交AB于点E,交AC于点F,过点O作
交AB于点E,交AC于点F,过点O作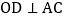 于D,下列四个结论.
于D,下列四个结论.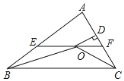
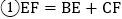
 点O到
点O到 各边的距离相等
各边的距离相等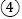 设
设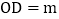 ,
,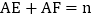 ,则
,则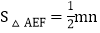 ,正确的结论有
,正确的结论有
 个.
个.A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边
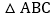 所在平面内有点P,且使得
所在平面内有点P,且使得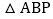 ,
, ,
,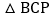 均为等腰三角形,则符合条件的点P共有______个
均为等腰三角形,则符合条件的点P共有______个
相关试题

