【题目】在等边![]() 所在平面内有点P,且使得
所在平面内有点P,且使得![]() ,
,![]() ,
,![]() 均为等腰三角形,则符合条件的点P共有______个
均为等腰三角形,则符合条件的点P共有______个![]()
参考答案:
【答案】10
【解析】
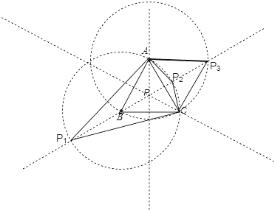
过B点作![]() 的中垂线,可知在三角形内有一点P满足
的中垂线,可知在三角形内有一点P满足![]() 、
、![]() 、
、![]() 都是等腰三角形,根据等腰三角形的性质可以做两个圆,圆B和圆A,从而可以得出一条中垂线上有四个点满足
都是等腰三角形,根据等腰三角形的性质可以做两个圆,圆B和圆A,从而可以得出一条中垂线上有四个点满足![]() 、
、![]() 、
、![]() 都是等腰三角形,而三角形内部的一点是重合的,所以可以得出共有10个点.
都是等腰三角形,而三角形内部的一点是重合的,所以可以得出共有10个点.
解:作三边的中垂线,交点P肯定是其中之一,以B为圆心,BA为半径画圆,交AC的中垂线于![]() 、
、![]() 两点,作
两点,作![]() 、
、![]() 、
、![]() ,它们也都是等腰三角形,因此
,它们也都是等腰三角形,因此![]() 、
、![]() 是具有题目所说的性质的点;
是具有题目所说的性质的点;
以A为圆心,BA为半径画圆,交AC的中垂线于点![]() 、
、![]() 也必具有题目所说的性质.
也必具有题目所说的性质.
依此类推,在![]() 的其余两条中垂线上也存在这样性质的点,所以这些点一共有:
的其余两条中垂线上也存在这样性质的点,所以这些点一共有:![]() 个.
个.
故答案为10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知射线CB//OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
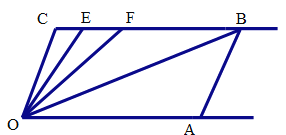
(1)求∠EOB的度数.(直接写出结果,无需解答过程)
∠EOB=__________°
(2)若在OC右侧左右平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,请找出变化规律;若不变,请求出这个比值.
(3)在OC右侧左右平行移动AB的过程中,是否存在使∠OEC=∠OBA的情况?若存在,请直接写出∠OEC度数;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:如图①,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
特例探究:如图②,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC, CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;
归纳证明:如图③,点BC在∠MAN的边AM、AN上,点EF在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC, ∠1=∠2=∠BAC.求证:△ABE≌△CAF;
拓展应用:如图④,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为 .(12分)




-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
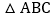 中,
中,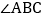 和
和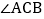 的平分线相交于点O,过O点作
的平分线相交于点O,过O点作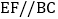 交AB于点E,交AC于点F,过点O作
交AB于点E,交AC于点F,过点O作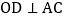 于D,下列四个结论.
于D,下列四个结论.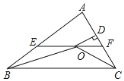
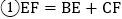
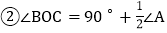
 点O到
点O到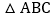 各边的距离相等
各边的距离相等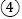 设
设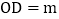 ,
,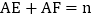 ,则
,则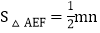 ,正确的结论有
,正确的结论有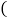
 个.
个.A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】济宁市“五城同创”活动中,一项绿化工程由甲、乙两工程队承担.已知甲工程队单独完成这项工作需120天,甲工程队单独工作30天后,乙工程队参与合做,两队又共同工作了36天完成.
(1)求乙工程队单独完成这项工作需要多少天?
(2)因工期的需要,将此项工程分成两部分,甲做其中一部分用了x天完成,乙做另一部分用了y天完成,其中x、y均为正整数,且x<46,y<52,求甲、乙两队各做了多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知DC∥FP,∠1=∠2,∠FED=28,∠AGF=80,FH平分∠EFG.
(1)说明:DC∥AB;
(2)求∠PFH的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(﹣3,2),(b,m),(c,m),则点E的坐标是( )
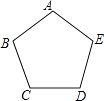
A.(2,﹣3)
B.(2,3)
C.(3,2)
D.(3,﹣2)
相关试题

