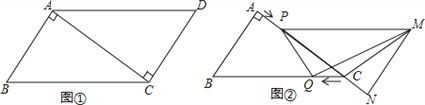
【题目】已知,如图①,在ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿CB方向匀速移动,速度为1cm/s,当△PNM停止平移时,点Q也停止移动,如图②,设移动时间为t(s)(0<t<4),连接PQ,MQ,MC,解答下列问题:
(1)当t为何值时,PQ∥MN?
(2)设△QMC的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S△QMC:S四边形ABQP=1:4?若存在,求出t的值;若不存在,请说明理由.
(4)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
参考答案:
【答案】t=![]() ;y=-
;y=-![]() ;1:4;t=
;1:4;t=![]()
【解析】试题分析: ![]() 当PQ∥MN时,可得:
当PQ∥MN时,可得: ![]() ,从而得到:
,从而得到: ![]() ,解方程求出
,解方程求出![]() 的值;
的值;
![]() 作
作![]() 于点
于点![]() ,则可以得到
,则可以得到![]() ,根据相似三角形的性质可以求出
,根据相似三角形的性质可以求出![]() ,
, ![]() ,利用三角形的面积公式求出
,利用三角形的面积公式求出![]() 与
与![]() 的关系式;
的关系式;
![]() 根据S△QMC:
根据S△QMC: ![]() 可以得到关于
可以得到关于![]() 的方程,解方程求出
的方程,解方程求出![]() 的值;
的值;
![]() 作
作![]() 于点
于点![]() ,
, ![]() 于点
于点![]() ,则△CPD∽△CBA,利用相似三角形的性质可以得到:
,则△CPD∽△CBA,利用相似三角形的性质可以得到: ![]() ,解方程求出
,解方程求出![]() 的值.
的值.
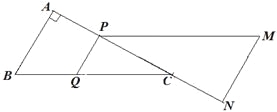
试题解析:(1)如图所示,
若PQ∥MN,则有![]() ,
,
∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
即![]() ,
,
解得![]() .
.
(2)如图所示,
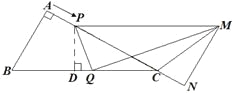
作![]() 于点
于点![]() ,则△CPD∽△CBA,
,则△CPD∽△CBA,
∴![]() ,
,
∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]()
又∵![]() ,
,
∴△QMC的面积为: ![]()
(3)存在![]() 时,使得S△QMC:
时,使得S△QMC: ![]() .
.
理由如下:
∵PM∥BC
∴![]()
∵S△QMC: ![]() ,
,
∴S△PQC: S△ABC=1:5,
∵![]()
.∴![]()
∴![]()
∴![]()
∴存在当![]() 时,S△QMC:
时,S△QMC: ![]() ;
;
(4)存在某一时刻![]() ,使
,使![]() .
.
理由如下:
如图所示,
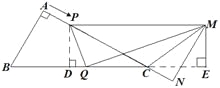
作![]() 于点
于点![]() ,
, ![]() 于点
于点![]() ,则△CPD∽△CBA,
,则△CPD∽△CBA,
∴![]() ,
,
∵![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
, ![]() .
.
∵PQ⊥MQ,
∴△PDQ∽△QEM,
∴![]() ,
,
即![]()
∵![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
, ![]() (舍去)
(舍去)
∴当![]() 时,使PQ⊥MQ.
时,使PQ⊥MQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=
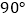 ,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
A. 1个
B. 2个
C. 3个
D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国政府从2007年起对职业中专在校生给予生活补贴,每位在校生每年补贴1500元某市预计2008年职业中专在校生人数是2007年的1.2倍,于是要在2007年的基础上增加补贴600万元。2008年该市职业中专在校生有多少万人?补贴多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
(1)求证:AD=CE;
(2)求∠DFC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定个人发表文章、出版图书获得稿费的纳税计算方法是:(l)稿费不高于800元的不纳税;(2)稿费高于800元又不高于4000元的,减除其中的800元,其余部分按20%纳税:(3)稿费高于4000元,减除稿酬的20%,其余部分按20%纳税.今知丁老师获得一笔稿费,并缴纳个人所得税600元,问:丁老师的这笔稿费有多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中:①∠A+∠B=∠C;②∠A﹕∠B﹕∠C=1﹕2﹕3;③∠A=
 ∠B=
∠B= ∠C;④∠A=∠B=2∠C;⑤∠A=∠B=
∠C;④∠A=∠B=2∠C;⑤∠A=∠B= ∠C,能确定△ABC为直角三角形的条件有( )
∠C,能确定△ABC为直角三角形的条件有( )A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蓄水池的排水管每小时排水8m3,6小时可将满池水全部排空.
(1)蓄水池的容积是____________ m3;
(2)如果增加排水管,使每小时排水量达到Q(m3),那么将满池水排空所需时间为t(小时),则Q与t之间关系式为____________;
(3)如果准备在5小时内将满池水排空,那么每小时的排水量至少为____________ m3/小时;
(4)已知排水管最多为每小时12m3,则至少____________小时可将满池水全部排空.
相关试题

