【题目】如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
(1)求证:AD=CE;
(2)求∠DFC的度数.

参考答案:
【答案】(1)证明见解析(2)60°
【解析】试题分析:(1)根据△ABC是等边三角形,得到∠BAC=∠B=60°,AB=AC,再根据AE=BD可以利用SAS证得△AEC≌△BDA,从而证得AD=CE.
(2)根据△AEC≌△BDA得到∠ACE=∠BAD,然后求得∠DFC=∠FAC+∠ACE=∠FAC+∠BAD=60°,从而求得其正弦值.
试题解析:
证明:(1)在等边△ABC中,AB=BA,∠B=∠CAE
∴在△ACE和△BAD中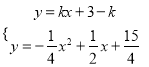
∴△ACE≌△BAD(SAS)
∴AD=CE
(2)∵△ACE≌△BAD(已证)
∴∠BAD=∠ACE,
而∠DFC=∠DAC+∠ACE
∴∠DFC=∠DAC+∠BAD=∠BAC=60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a>b,则下列各式中正确的是( )
A.a﹣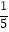 <b﹣
<b﹣ 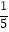
B.﹣4a>﹣4b
C.﹣2a+1<﹣2b+1
D.a2>b2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的边数增加1,那么它的内角和增加( ).
A. 0° B. 90° C. 180° D. 360°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是( )

A. 25° B. 30° C. 35° D. 40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A1(1,1),A2(2,4),A3(3,9),A4(4,16),…,用你发现的规律确定点A9的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠ACD是△ABC的外角, BE平分∠ABC, CE平分∠ACD,且BE、CE交于点E。试找出∠A与∠E的关系。
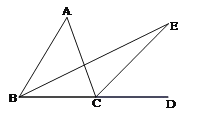
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个四边形四个内角度数之比是2∶2∶3∶5,那么这四个内角中( ).
A. 只有一个直角 B. 只有一个锐角 C. 有两个直角 D. 有两个钝角
相关试题

