【题目】规定:[m]为不大于m的最大整数;
(1)填空:[3.2]= ,[﹣4.8]= ;
(2)已知:动点C在数轴上表示数a,且﹣2≤[a]≤4,则a的取值范围 ;
(3)如图:OB=1,AB⊥OB,且AB=10,动点D在数轴上表示的数为t,设AD﹣BD=n,且6≤[n]≤7,求t的取值范围.

参考答案:
【答案】(1)3,-5;(2)﹣2≤a<5;(3)﹣![]() ≤t<﹣
≤t<﹣![]() 或
或![]() <t≤
<t≤![]() .
.
【解析】
(1)根据[m]为不大于m的最大整数数即可求解;
(2)根据[m]为不大于m的最大整数,可得﹣2≤a<5即可求解;
(3)分两种情形:当点D在点B的右边时,当点D在点B的左边时分别求解即可.
解:(1)[3.2]=3,[﹣4.8]=﹣5.
故答案为3,﹣5.
(2)∵﹣2≤[a]≤4
∴﹣2≤a<5.
(3)如图,当点D在点B的右边时,
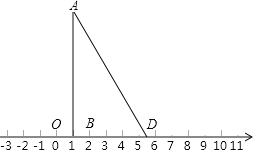
∵6≤[n]≤7,
∴6≤n<8,
当n=8时,![]() ﹣(t﹣1)=8,
﹣(t﹣1)=8,
解得t=![]() ,
,
当n=6时,![]() ﹣(t﹣1)=8,
﹣(t﹣1)=8,
解得t=![]() ,
,
观察图象可知,![]() <t≤
<t≤![]() .
.
当点D在点B的左边时,同法可得﹣![]() ≤t<﹣
≤t<﹣![]() ,
,
综上所述,满足条件的t的值为﹣![]() ≤t<﹣
≤t<﹣![]() 或
或![]() <t≤
<t≤![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)
 .
.(2)
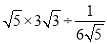 .
.(3)
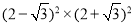 .
.(4)
 .(利用幂的运算性质计算)
.(利用幂的运算性质计算)(5)
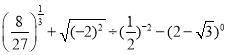 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=
 BC,连结OE.下列结论:
BC,连结OE.下列结论:①∠CAD=30°;②SABCD=AB·AC;③OB=AB;④OE=
 BC,成立的结论有______.(填序号)
BC,成立的结论有______.(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,O为菱形ABCD的对称中心,已知C(2,0),D(0,﹣1),N为线段CD上一点(不与C、D重合).

(1)求以C为顶点,且经过点D的抛物线解析式;
(2)设N关于BD的对称点为N1,N关于BC的对称点为N2,求证:△N1BN2∽△ABC;
(3)求(2)中N1N2的最小值;
(4)过点N作y轴的平行线交(1)中的抛物线于点P,点Q为直线AB上的一个动点,且∠PQA=∠BAC,求当PQ最小时点Q坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
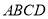 中,
中, 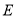 为对角线
为对角线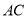 ,
, 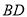 的交点,经过点
的交点,经过点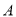 和点
和点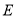 作⊙
作⊙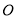 ,分别交
,分别交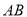 ,
, 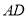 于点
于点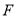 ,
, 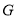 .已知正方形边长为
.已知正方形边长为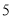 ,⊙
,⊙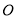 的半径为
的半径为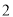 ,则
,则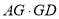 的值为__________.
的值为__________.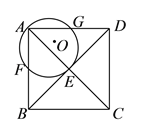
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,∠1+∠2=180°.请填写∠CGD=∠CAB的理由.
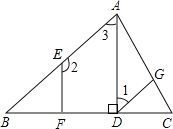
解:因为AD⊥BC,EF⊥BC(______ )
所以∠ADC=90°,∠EFD=90°(______ )
得∠ADC=∠EFD(等量代换),
所以AD∥EF(______ )
得∠2+∠3=180°(______ )
由∠1+∠2=180°(______ )
得∠1=∠3(______ )
所以DG∥AB(______ )
所以∠CGD=∠CAB(______ )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD的反向延长线交y轴负半轴于点E,双曲线
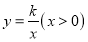 的图象经过点A,若S△BEC=3,则k等于( )
的图象经过点A,若S△BEC=3,则k等于( )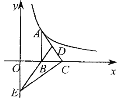
A.12B.6C.3D.2
相关试题

