【题目】如图,已知AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,∠1+∠2=180°.请填写∠CGD=∠CAB的理由.
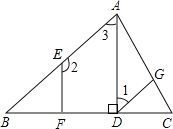
解:因为AD⊥BC,EF⊥BC(______ )
所以∠ADC=90°,∠EFD=90°(______ )
得∠ADC=∠EFD(等量代换),
所以AD∥EF(______ )
得∠2+∠3=180°(______ )
由∠1+∠2=180°(______ )
得∠1=∠3(______ )
所以DG∥AB(______ )
所以∠CGD=∠CAB(______ )
参考答案:
【答案】已知 垂直定义 同位角相等,两直线平行 两直线平行,同旁内角互补 已知 同角的补角相等 内错角相等,两直线平行 两直线平行,同位角相等
【解析】
求出AD∥EF,根据平行线的性质得出∠2+∠3=180°,求出∠1=∠3,根据平行线的判定得出DG∥AB,根据平行线的性质得出∠CGD=∠CAB即可.
解:∵AD⊥BC,EF⊥BC(已知),
∴∠ADC=90°,∠EFC=90°(垂直定义),
∴∠ADC=∠EFD,
∴AD∥EF(同位角相等,两直线平行),
∴∠2+∠3=180°(两直线平行,同旁内角互补),
∵∠1+∠2=180°(已知),
∴∠1=∠3(同角的补角相等),
∴DG∥AB(内错角相等,两直线平行),
∴∠CGD=∠CAB(两直线平行,同位角相等).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,O为菱形ABCD的对称中心,已知C(2,0),D(0,﹣1),N为线段CD上一点(不与C、D重合).

(1)求以C为顶点,且经过点D的抛物线解析式;
(2)设N关于BD的对称点为N1,N关于BC的对称点为N2,求证:△N1BN2∽△ABC;
(3)求(2)中N1N2的最小值;
(4)过点N作y轴的平行线交(1)中的抛物线于点P,点Q为直线AB上的一个动点,且∠PQA=∠BAC,求当PQ最小时点Q坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定:[m]为不大于m的最大整数;
(1)填空:[3.2]= ,[﹣4.8]= ;
(2)已知:动点C在数轴上表示数a,且﹣2≤[a]≤4,则a的取值范围 ;
(3)如图:OB=1,AB⊥OB,且AB=10,动点D在数轴上表示的数为t,设AD﹣BD=n,且6≤[n]≤7,求t的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
 中,
中,  为对角线
为对角线 ,
, 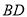 的交点,经过点
的交点,经过点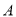 和点
和点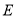 作⊙
作⊙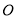 ,分别交
,分别交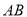 ,
, 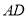 于点
于点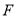 ,
, 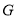 .已知正方形边长为
.已知正方形边长为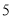 ,⊙
,⊙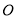 的半径为
的半径为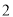 ,则
,则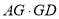 的值为__________.
的值为__________.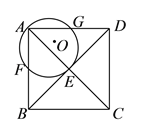
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD的反向延长线交y轴负半轴于点E,双曲线
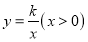 的图象经过点A,若S△BEC=3,则k等于( )
的图象经过点A,若S△BEC=3,则k等于( )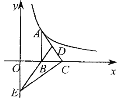
A.12B.6C.3D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:
 .
.(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)
-
科目: 来源: 题型:
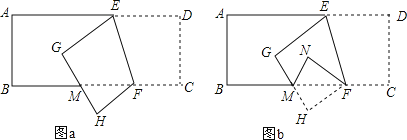
查看答案和解析>>【题目】如图a,已知长方形纸带ABCD,AB∥CD,AD∥BC,∠BFE=70°,将纸带沿EF折叠后,点C、D分别落在H、G的位置,再沿BC折叠成图b.
(1)图a中,∠AEG=______°;
(2)图a中,∠BMG=______°;
(3)图b中,∠EFN=______°.
相关试题

