【题目】如图,平面直角坐标系中,O为菱形ABCD的对称中心,已知C(2,0),D(0,﹣1),N为线段CD上一点(不与C、D重合).

(1)求以C为顶点,且经过点D的抛物线解析式;
(2)设N关于BD的对称点为N1,N关于BC的对称点为N2,求证:△N1BN2∽△ABC;
(3)求(2)中N1N2的最小值;
(4)过点N作y轴的平行线交(1)中的抛物线于点P,点Q为直线AB上的一个动点,且∠PQA=∠BAC,求当PQ最小时点Q坐标.
参考答案:
【答案】(1)y=﹣![]() (x﹣2)2(2)证明见解析(3)
(x﹣2)2(2)证明见解析(3)![]() (4)
(4)![]()
【解析】试题分析:(1)用待定系数法求,即可;
(2)由对称的特点得出∠N1BN2=2∠DBC结合菱形的性质即可;
(3)先判定出,当BN⊥CD时,BN最短,再利用△ABC∽△N1BN2得到比例式,求解,即可;
(4)先建立PE=![]() m2﹣
m2﹣![]() m+2函数解析式,根据抛物线的特点确定出最小值.
m+2函数解析式,根据抛物线的特点确定出最小值.
试题解析:(1)由已知,设抛物线解析式为y=a(x﹣2)2
把D(0,﹣1)代入,得a=﹣![]()
∴y=﹣![]() (x﹣2)2
(x﹣2)2
(2)如图1,连结BN.
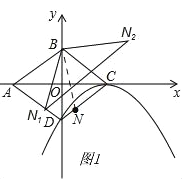
∵N1,N2是N的对称点
∴BN1=BN2=BN,∠N1BD=∠NBD,∠NBC=∠N2BC
∴∠N1BN2=2∠DBC
∵四边形ABCD是菱形
∴AB=BC,∠ABC=2∠DBC
∴∠ABC=∠N1BN2, ![]()
∴△ABC∽△N1BN2
(3)∵点N是CD上的动点,
∴点到直线的距离,垂线段最短,
∴当BN⊥CD时,BN最短.
∵C(2,0),D(0,﹣1)
∴CD=![]() ,
,
∴BNmin=![]() ,
,
∴BN1min=BNmin=![]() ,
,
∵△ABC∽△N1BN2
∴![]() ,
,
N1N2min=![]() ,
,
(4)如图2,
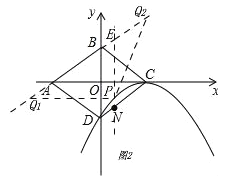
过点P作PE⊥x轴,交AB于点E.
∵∠PQA=∠BAC
∴PQ1∥AC
∵菱形ABCD中,C(2,0),D(0,﹣1)
∴A(﹣2,0),B(0,1)
∴lAB:Y=![]() x+1
x+1
不妨设P(m,﹣![]() (m﹣2)2),则E(m,
(m﹣2)2),则E(m, ![]() m+1)
m+1)
∴PE=![]() m2﹣
m2﹣![]() m+2
m+2
∴当m=1时, ![]()
此时,PQ1最小,最小值为![]() =
=![]() ,
,
∴PQ1=PQ2=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】光的速度约是3×105km/s,太阳光照射到地球表面所需的时间约是5×102s,那么地球与太阳之间的距离约是(用科学记数法表示)( )
A. 1.5×107km B. 1.5×108km C. 15×108km D. 15×107km
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于有序数对(a,b)定义如下的运算””:(a,b)(c,d)=(ac+bd,ad﹣bc),那么(a,b)(0,1)等于( )
A. (b,a)B. (﹣b,﹣a)C. (a,﹣b)D. (﹣a,b)
-
科目: 来源: 题型:
查看答案和解析>>【题目】现从10个红球,6个白球,4个黄球中任取m个球,并给出以下说法:①若m≥11,则任取的m个球中至少1个红球的概率为1;②若m≥15,则任取的m个球中至少1个白球的概率为1;③若m≥17,则任取的m个球中至少1个黄球的概率为1.其中错误的说法有( )
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠α与∠β互为补角,则下列式子成立的是( )
A.α-β=90° B.α+β=90° C.α-β=180° D.α+β=180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】若过点P和点A(3,2)的直线平行于x轴,过点P和B(﹣1,﹣2)的直线平行于y轴,则点P的坐标为( )
A. (﹣1,2 )B. (﹣2,2)C. (3,﹣1)D. (3,﹣2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为贯彻政府报告中“大众创业、万众创新”的精神,某镇对辖区内所有的小微企业按年利润w(万元)的多少分为以下四个类型:A类(w<10),B类(10≤w<20),C类(20≤w<30),D类(w≥30),该镇政府对辖区内所有小微企业的相关信息进行统计后,绘制成以下条形统计图和扇形统计图,请你结合图中信息解答下列问题:
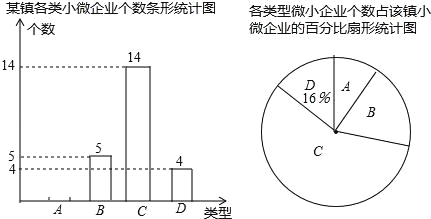
(1)该镇本次统计的小微企业总个数是 ,扇形统计图中B类所对应扇形圆心角的度数为 度,请补全条形统计图;
(2)为了进一步解决小微企业在发展中的问题,该镇政府准备召开一次座谈会,每个企业派一名代表参会.计划从D类企业的4个参会代表中随机抽取2个发言,D类企业的4个参会代表中有2个来自高新区,另2个来自开发区.请用列表或画树状图的方法求出所抽取的2个发言代表都来自高新区的概率.
相关试题

