【题目】(1)![]() .
.
(2)![]() .
.
(3)![]() .
.
(4)![]() .(利用幂的运算性质计算)
.(利用幂的运算性质计算)
(5)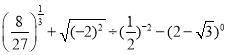 .
.
参考答案:
【答案】(1)![]() ;(2)90
;(2)90![]() ;(3)1;(4)4;(5)
;(3)1;(4)4;(5)![]() ;
;
【解析】
(1)根据二次根式的加减运算法则即可求出答案.
(2)根据二次根式的乘除运算法则即可求出答案.
(3)先逆用积的乘方法则,然后根据平方差公式即可求出答案.
(4)先化成分数指数幂,然后再转化成同底数幂,再利用同底数幂的乘除法法则即可得出答案.
(5)根据分数指数幂的意义以及负整数指数幂的意义即可求出答案.
解:(1)原式=(2+3-4)![]()
=![]() ;
;
(2)原式=![]() ×3
×3![]() ×6
×6![]()
=5×3![]() ×6
×6
=90![]() ;
;
(3)原式=[(2-![]() )(2+
)(2+![]() )]2
)]2
=(4-3)2
=1;
(4)原式=![]() ×
×![]() ÷
÷![]()
=![]() ×
×![]() ÷
÷![]()
=22;
=4;
(5)原式=![]() +2÷4-1
+2÷4-1
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张矩形纸片沿着AE折叠后,点D恰好与BC边上的点F重合,已知AB=6cm,BC=10cm,则EC的长度为_____cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面坐标系中,
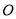 为原点,直线
为原点,直线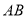 交
交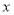 轴正半轴于点
轴正半轴于点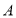 ,交
,交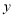 轴正半轴于点
轴正半轴于点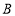 .
.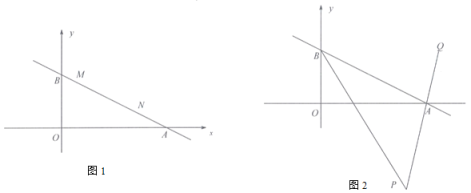
(1) 如图1,直线
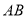 上有
上有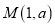 和
和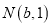 两点,
两点,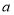 的相反数是
的相反数是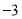 ,
,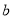 是
是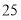 的算术平方根,求:
的算术平方根,求:①
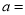 ____ ;
____ ; 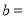 _____ ; ②点
_____ ; ②点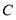 在
在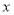 轴正半轴上运动,使得
轴正半轴上运动,使得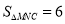 ,则点
,则点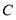 的坐标为 .
的坐标为 .(2)如图2, 若
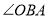 的平分线
的平分线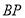 与
与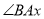 的平分线
的平分线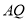 反向延长线交于点
反向延长线交于点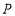 ,设
,设 ,求证:
,求证: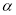 的值为定值;
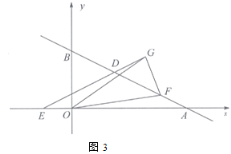
的值为定值;(3)如图3,
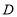 在直线
在直线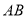 上,
上, 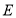 在
在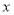 轴上,在
轴上,在 中,始终满足以下条件:
中,始终满足以下条件: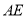 为最大边,
为最大边, 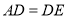 ,当
,当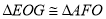 时,求
时,求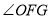 的取值范围.
的取值范围. -
科目: 来源: 题型:
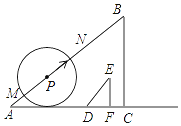
查看答案和解析>>【题目】如图,已知Rt△ABC的直角边AC与Rt△DEF的直角边DF在同一条直线上,且AC=60cm,BC=45cm,DF=6cm,EF=8cm.现将点C与点F重合,再以4cm/s的速度沿
CA方向移动△DEF;同时,点P从点A出发,以5cm/s的速度沿AB方向移动.设移动时间为t(s),以点P为圆心,3t(cm)长为半径的⊙P与直线AB相交于点M,N,当点F与点A重合时,△DEF与点P同时停止移动,在移动过程中:
(1)连接ME,当ME∥AC时,t=________s;
(2)连接NF,当NF平分DE时,求t的值;
(3)是否存在⊙P与Rt△DEF的两条直角边所在的直线同时相切的时刻?若存在,求出t的值;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=
 BC,连结OE.下列结论:
BC,连结OE.下列结论:①∠CAD=30°;②SABCD=AB·AC;③OB=AB;④OE=
 BC,成立的结论有______.(填序号)
BC,成立的结论有______.(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,O为菱形ABCD的对称中心,已知C(2,0),D(0,﹣1),N为线段CD上一点(不与C、D重合).

(1)求以C为顶点,且经过点D的抛物线解析式;
(2)设N关于BD的对称点为N1,N关于BC的对称点为N2,求证:△N1BN2∽△ABC;
(3)求(2)中N1N2的最小值;
(4)过点N作y轴的平行线交(1)中的抛物线于点P,点Q为直线AB上的一个动点,且∠PQA=∠BAC,求当PQ最小时点Q坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定:[m]为不大于m的最大整数;
(1)填空:[3.2]= ,[﹣4.8]= ;
(2)已知:动点C在数轴上表示数a,且﹣2≤[a]≤4,则a的取值范围 ;
(3)如图:OB=1,AB⊥OB,且AB=10,动点D在数轴上表示的数为t,设AD﹣BD=n,且6≤[n]≤7,求t的取值范围.

相关试题

