【题目】如图,抛物线![]() 经过
经过![]() 、
、![]() 、
、![]() 三点.
三点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 如图①,在抛物线的对称轴上是否存在点
如图①,在抛物线的对称轴上是否存在点![]() ,使得四边形
,使得四边形![]() 的周长最小?若存在,求出四边形
的周长最小?若存在,求出四边形![]() 周长的最小值;若不存在,请说明理由.
周长的最小值;若不存在,请说明理由.
![]() 如图②,点
如图②,点![]() 是线段
是线段![]() 上一动点,连接
上一动点,连接![]() ,在线段
,在线段![]() 上是否存在这样的点
上是否存在这样的点![]() ,使
,使![]() 为等腰三角形且
为等腰三角形且![]() 为直角三角形?若存在,求点
为直角三角形?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

参考答案:
【答案】![]()
![]() .
.![]() 在抛物线的对称轴上存在点
在抛物线的对称轴上存在点![]() ,使得四边形
,使得四边形![]() 的周长最小,四边形
的周长最小,四边形![]() 周长的最小值为
周长的最小值为![]() .
.![]() 在线段
在线段![]() 上存在这样的点
上存在这样的点![]() ,使
,使![]() 为等腰三角形且
为等腰三角形且![]() 为直角三角形,点
为直角三角形,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)把点A(1,0)、B(4,0)、C(0,3)三点的坐标代入函数解析式,利用待定系数法求解;
(2)A、B关于对称轴对称,连接BC,则BC与对称轴的交点即为所求的点P,此时PA+PC=BC,四边形PAOC的周长最小值为:OC+OA+BC;根据勾股定理求得BC,即可求得;
(3)分两种情况分别讨论,即可求得.
![]() 由已知得
由已知得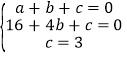 解得
解得 .
.
所以,抛物线的解析式为![]() .
.
![]() ∵
∵![]() 、
、![]() 关于对称轴对称,如图
关于对称轴对称,如图![]() ,连接
,连接![]() ,
,

∴![]() 与对称轴的交点即为所求的点
与对称轴的交点即为所求的点![]() ,此时
,此时![]() ,
,
∴四边形![]() 的周长最小值为:
的周长最小值为:![]() ,
,
∵![]() 、
、![]() 、
、![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ;
;
∴在抛物线的对称轴上存在点![]() ,使得四边形
,使得四边形![]() 的周长最小,四边形
的周长最小,四边形![]() 周长的最小值为
周长的最小值为![]() .
.
![]() ∵
∵![]() 、
、![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
①当![]() 时,如图
时,如图![]() ,设
,设![]() ,
,
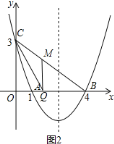
∵![]() ,
,
∴只能![]() ,
,
∵![]() 轴,
轴,
∴![]() ,
,
∴![]() ,即
,即![]() ,解得
,解得![]() ,
,
代入![]() 得,
得,![]() ,解得
,解得![]() ,
,
∴![]() ;
;
②当![]() 时,如图
时,如图![]() ,
,
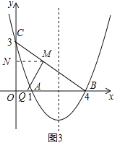
∵![]() ,
,
∴只能![]() ,
,
设![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,解得
,解得![]() ,
,
作![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
综上,在线段![]() 上存在这样的点
上存在这样的点![]() ,使
,使![]() 为等腰三角形且
为等腰三角形且![]() 为直角三角形,点
为直角三角形,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少________个时,网球可以落入桶内.
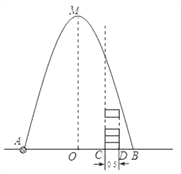
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )

A. 130°B. 120°C. 110°D. 100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,672可以写成6×102+7×10+2,对于多项式而言,关于某一字母的多项式都可以按这个字母的降幂排列比如7x+2+6x2可以写成6x2+7x+2.在解决多项式相除的问题时,我们通过对比发现,可以类比多位数的除法,用竖式进行计算,例如:(7x+2+6x2)÷(2x+1),仿照672÷21计算如图,因此:(7x+2+6x2)÷(2x+1)=3x+2.根据阅读材料,

(1)试判断:x3﹣x2﹣5x﹣3能否被x+1整除_____,(请用“能”或“不能”填空)
(2)多项式2x5+3x3+5x2﹣2x+10除以x2+1的商式是_____,余式是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】蔬菜基地种植某种蔬菜,由市场行情分析知,1月份至6月份这种蔬菜的上市时间
 (月份)与市场售价
(月份)与市场售价 (元/千克)的关系如下表:
(元/千克)的关系如下表:上市时间
 (月份)
(月份)1
2
3
4
5
6
市场售价
 (元/千克)
(元/千克)10.5
9
7.5
6
4.5
3
这种蔬菜每千克的种植成本
 (元/千克)与上市时间
(元/千克)与上市时间 (月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).
(月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).(1)写出上表中表示的市场售价
 (元/千克)关于上市时间
(元/千克)关于上市时间 (月份)的函数关系式;
(月份)的函数关系式;(2)若图中抛物线过
 点,写出抛物线对应的函数关系式;
点,写出抛物线对应的函数关系式;(3)由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值为多少?(收益=市场售价-种植成本)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
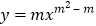 是
是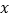 的二次函数.
的二次函数.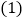 当
当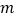 取何值时,该二次函数的图象开口向下?
取何值时,该二次函数的图象开口向下?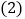 在
在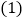 的条件下
的条件下①当
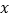 取何值时,
取何值时, ?
? ?
?②当
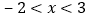 时,求
时,求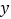 的取值范围;
的取值范围;③当一
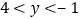 时,求
时,求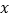 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,△ABC的三个顶点分别落在边长为1的正方形格上,
(1)分别写出A、B、C三点坐标;
(2)△DEF可以看作是△ABC经过若干次的图形变化(轴对称、平移)得到的,写出一种由△ABC得到△DEF的过程,并体现在坐标系中.

相关试题

