【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )

A. 130°B. 120°C. 110°D. 100°
参考答案:
【答案】B
【解析】
根据要使△AMN的周长最小,即利用点的对称,让三角形的三边在同一直线上,作出A关于BC和ED的对称点A′,A″,即可得出∠AA′M+∠A″=∠HAA′=60°,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″)即可得出答案:
如图,作A关于BC和ED的对称点A′,A″,连接A′A″,交BC于M,交CD于N,

则A′A″即为△AMN的周长最小值。作DA延长线AH。
∵∠BAD=120°,∴∠HAA′=60°。
∴∠AA′M+∠A″=∠HAA′=60°。
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,
∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×60°=120°。
故选B。
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的三个内角A,B,C所对的边分别是
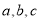 ,下列条件中,不能判定△ABC是等腰三角形的是( )
,下列条件中,不能判定△ABC是等腰三角形的是( )A.a3,b3,c4B.a︰b︰c2︰3︰4
C.∠B50°,∠C80°D.∠A︰∠B︰∠C1︰1︰2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,E是AB的中点,AD//EC,∠AED=∠B.
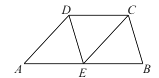
(1)求证:△AED≌△EBC;
(2)当AB=6时,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点D、F、E、G都在△ABC的边上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请在下面的空格处填写理由或数学式)

解:∵EF∥AD,(已知)
∴∠2= ( )
∵∠1=∠2,(已知)
∴∠1= ( )
∴ ∥ ,( )
∴∠AGD+ =180°,(两直线平行,同旁内角互补)
∵∠BAC=70°,(已知)
∴∠AGD= (等式性质)
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程: (1)x2-49=0 (2)3x2-7x=0 (3)(2x-1)2=9
(4)x2+3x-4=0 (5)(x+4)2=5(x+4) (6)x2+4x=2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠B=90 , BC=12,tanC=
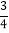 . 如果一质点P开始时在AB边的P0处,BP0=3.P第一步从P0跳到AC边的P1(第1次落点)处,且
. 如果一质点P开始时在AB边的P0处,BP0=3.P第一步从P0跳到AC边的P1(第1次落点)处,且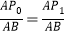 ;第二步从P1跳到BC边的P2(第2次落点)处,且
;第二步从P1跳到BC边的P2(第2次落点)处,且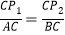 ;第三步从P2跳到AB边的P3(第3次落点)处,且
;第三步从P2跳到AB边的P3(第3次落点)处,且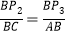 ;…;质点P按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2014与点P2015之间的距离为( )
;…;质点P按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2014与点P2015之间的距离为( )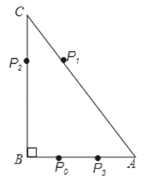
A. 6 B. 5 C. 4 D. 3
相关试题

