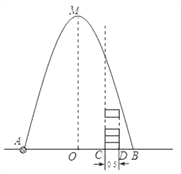
【题目】如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少________个时,网球可以落入桶内.
参考答案:
【答案】8
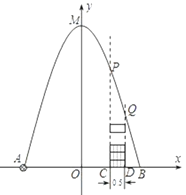
【解析】以点O为原点,AB所在直线为x轴建立直角坐标系(如图),
M(0,5),B(2,0),C(1,0),D(![]() ,0),
,0),
设抛物线的解析式为y=ax2+k,
抛物线过点M和点B,
则k=5,a=﹣![]() ,
,
∴抛物线解析式为:y=﹣![]() x2+5;
x2+5;
∴当x=1时,y=![]() ;
;
当x=![]() 时,y=
时,y=![]() ,
,
∴P(1, ![]() ),Q(
),Q(![]() ,
, ![]() )在抛物线上;
)在抛物线上;
设竖直摆放圆柱形桶m个时网球可以落入桶内,
由题意,得, ![]() ≤
≤![]() m≤
m≤![]() ,
,
解得:7![]() ≤m≤12
≤m≤12![]() ;
;
∵m为整数,
∴m的最小整数值为:8,
∴竖直摆放圆柱形桶至少8个时,网球可以落入桶内,
故答案为:8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
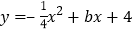 与
与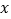 轴相交于
轴相交于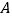 、
、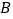 两点,与
两点,与 轴相交于点
轴相交于点 .若已知
.若已知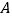 点的坐标为
点的坐标为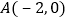 .点
.点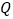 在抛物线的对称轴上,当
在抛物线的对称轴上,当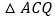 为等腰三角形时,点
为等腰三角形时,点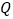 的坐标为________.
的坐标为________.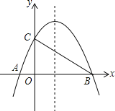
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:在
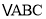 中,
中,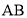 、
、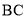 、
、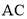 三边的长分别为
三边的长分别为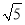 、
、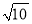 、
、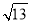 ,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为
,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为 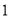 ),在网格中画出格点
),在网格中画出格点 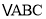 (即
(即 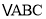 三个顶点都在小正方形的顶点处),如图所示,这样借用网格就能计算出它的面积.
三个顶点都在小正方形的顶点处),如图所示,这样借用网格就能计算出它的面积.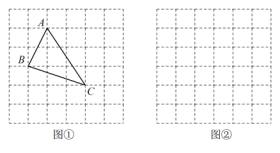
(1)请你直接写出
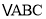 的面积为 .
的面积为 .(2)若
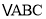 三边的长分别为
三边的长分别为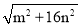 、
、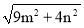 、
、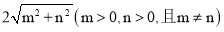 运用构图法求出这三角形的面积.
运用构图法求出这三角形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠BAD=∠CAD,则下列条件中不一定能使△ABD≌△ACD的是( )

A.∠B=∠CB.∠BDA=∠CDAC.AB=ACD.BD=CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )

A. 130°B. 120°C. 110°D. 100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,672可以写成6×102+7×10+2,对于多项式而言,关于某一字母的多项式都可以按这个字母的降幂排列比如7x+2+6x2可以写成6x2+7x+2.在解决多项式相除的问题时,我们通过对比发现,可以类比多位数的除法,用竖式进行计算,例如:(7x+2+6x2)÷(2x+1),仿照672÷21计算如图,因此:(7x+2+6x2)÷(2x+1)=3x+2.根据阅读材料,

(1)试判断:x3﹣x2﹣5x﹣3能否被x+1整除_____,(请用“能”或“不能”填空)
(2)多项式2x5+3x3+5x2﹣2x+10除以x2+1的商式是_____,余式是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 经过
经过 、
、 、
、 三点.
三点. 求抛物线的解析式;
求抛物线的解析式; 如图①,在抛物线的对称轴上是否存在点
如图①,在抛物线的对称轴上是否存在点 ,使得四边形
,使得四边形 的周长最小?若存在,求出四边形
的周长最小?若存在,求出四边形 周长的最小值;若不存在,请说明理由.
周长的最小值;若不存在,请说明理由. 如图②,点
如图②,点 是线段
是线段 上一动点,连接
上一动点,连接 ,在线段
,在线段 上是否存在这样的点
上是否存在这样的点 ,使
,使 为等腰三角形且
为等腰三角形且 为直角三角形?若存在,求点
为直角三角形?若存在,求点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
相关试题

