【题目】如图,PA、PB切⊙O于A、B, ![]() ,点C是⊙O上异于A、B的任意一点,则
,点C是⊙O上异于A、B的任意一点,则 ![]() = .
= . 
参考答案:
【答案】65°或115°
【解析】分两种情况:(1)当C在优弧AB上;(2)当C在劣弧AB上;连接OA、OB,在四边形PAOB中,∠OAP=∠OBP=90°,由内角和求得∠AOB的大小,然后根据圆周角定理即可求得答案(1)如图(1),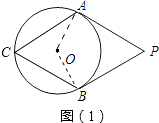
连接OA、OB.
在四边形PAOB中,由于PA、PB分别切⊙O于点A、B,
则∠OAP=∠OBP=90°;
由四边形的内角和定理,知
∠APB+∠AOB=180°;
又∵∠P=50°,
∴∠AOB=130°;
又∵∠ACB= ![]() ∠AOB(同弧所对的圆周角是所对的圆心角的一半),
∠AOB(同弧所对的圆周角是所对的圆心角的一半),
∴∠ACB=65°(2)如图(2),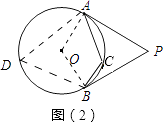
连接OA、OB,作圆周角∠ADB.
在四边形PAOB中,由于PA、PB分别切⊙O于点A、B,
则∠OAP=∠OBP=90°;
由四边形的内角和定理,知
∠APB+∠AOB=180°;
又∠P=50°,
∴∠AOB=130°;
∴∠ADB= ![]() ∠AOB=65°,
∠AOB=65°,
∴∠ACB=180°﹣∠ADB=115°.
∴∠ACB=65°或115°
【考点精析】通过灵活运用圆周角定理和圆内接四边形的性质,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,定点
 、
、 、
、 的坐标分别是(4,0)、(0,4)、(2,0),动点
的坐标分别是(4,0)、(0,4)、(2,0),动点 在第一象限,且到原点
在第一象限,且到原点 的距离为4个单位长度.
的距离为4个单位长度.(1)当点
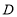 到两坐标轴的距离相等时,求
到两坐标轴的距离相等时,求 的面积;
的面积; (2)若点
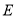 是线段
是线段 (不与点
(不与点 、
、 重合)上的动点,当
重合)上的动点,当 是等腰直角三角形时,求点
是等腰直角三角形时,求点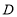 到
到 轴的距离.
轴的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
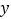 的图象开口向上,与 x轴的交点坐标是(1,0),对称轴x=-1.下列结论中,错误的是( )
的图象开口向上,与 x轴的交点坐标是(1,0),对称轴x=-1.下列结论中,错误的是( )
A.abc<0
B.b=2a
C.a+b+c=0
D.2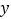
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图一,在△ABC中,AD是角平分线,AE是高,∠ABC=30°,∠ACB=70°.
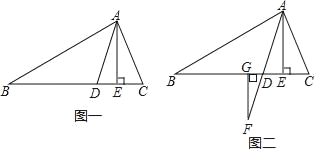
(1)求∠DAE的度数.
(2)如图二,若点F为AD延长线上一点,过点F作FG⊥BC于点G,求∠AFG的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来随着全国楼市的降温,商品房的价格开始呈现下降趋势,2012年某楼盘平均售价为5000元/平方米,2014年该楼盘平均售价为4050元/平方米.
(1)如果该楼盘2013年和2014年楼价平均下降率相同,求该楼价的平均下降率;
(2)按照(1)中楼价的下降速度,请你预测该楼盘2015年楼价平均是多少元/平方米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(1)求证:AM=AD+MC;
(2)若AD=4,求AM的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)在Rt△ABC中,∠BAC=
 ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
相关试题

