【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若AB=4+ ![]() ,BC=2
,BC=2 ![]() ,求⊙O的半径.
,求⊙O的半径.
参考答案:
【答案】
(1)证明:连接OA,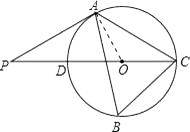
∵∠B=60°,
∴∠AOC=2∠B=120°,
又∵OA=OC,
∴∠OAC=∠OCA=30°,
又∵AP=AC,
∴∠P=∠ACP=30°,
∴∠OAP=∠AOC﹣∠P=90°,
∴OA⊥PA,
∴PA是⊙O的切线;
(2)解:过点C作CE⊥AB于点E.
在Rt△BCE中,∠B=60°,BC=2 ![]() ,
,
∴BE= ![]() BC=
BC= ![]() ,CE=3,
,CE=3,
∵AB=4+ ![]() ,
,
∴AE=AB﹣BE=4,
∴在Rt△ACE中,AC= ![]() =5,
=5,
∴AP=AC=5.
∴在Rt△PAO中,OA= ![]() ,
,
∴⊙O的半径为 ![]() .
.
【解析】(1)连接半径,利用圆周角定理和等腰三角形的性质可证出OA⊥PA,进而证出PA是⊙O的切线;(2)通过过C作垂线把∠B放到直角三角形中,利用60度角的三角函数,求出AC,进而求出⊙O的半径.
【考点精析】本题主要考查了圆周角定理和切线的判定定理的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于
 的方程
的方程  的解是
的解是  =
=  ,
,  =
=  (
(  、
、  、
、  为常数,
为常数, 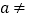 0),则方程
0),则方程  的解是 .
的解是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个角的两边与另一个角的两边分别平行,那么这两个角的大小有什么数量关系?请说明理由。(要求:画出图形,并写出已知,求证,证明过程)。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC, EF∥BC,∠AEF=143°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为多少米?(结果精确到0.1.参考数据:sin 37° ≈ 0.60,cos 37° ≈ 0.80,tan 37° ≈ 0.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题学习】小芸在小组学习时问小娟这样一个问题:已知α为锐角,且sinα=
 ,求sin2α的值.小娟是这样给小芸讲解的:
,求sin2α的值.小娟是这样给小芸讲解的:
构造如图1所示的图形,在⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°,作CD⊥AB于D.设∠BAC=α,则sinα= ,可设BC=x,则AB=3x,….
,可设BC=x,则AB=3x,….
(1)【问题解决】
请按照小娟的思路,利用图1求出sin2α的值;(写出完整的解答过程)
(2)如图2,已知点M,N,P为⊙O上的三点,且∠P=β,sinβ= ,求sin2β的值.
,求sin2β的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点,与y轴交于C点,对称轴与抛物线相交于点M,与x轴相交于点N.点P是线段MN上的一动点,过点P作PE⊥CP交x轴于点E.
(1)直接写出抛物线的顶点M的坐标是 .
(2)当点E与点O(原点)重合时,求点P的坐标.
(3)点P从M运动到N的过程中,求动点E的运动的路径长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,大正方形的边长为4厘米,小正方形的边长为2厘米,状态如图所示。大正方形固定不动,把小正方形以1厘米∕秒的速度向大正方形的内部沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S厘米2,完成下列问题:

(1)平移到1.5秒时,重叠部分的面积为 厘米2.
(2)求小正方形在平移过程中,S与t的关系式。
相关试题

