【题目】【问题学习】小芸在小组学习时问小娟这样一个问题:已知α为锐角,且sinα= ![]() ,求sin2α的值.小娟是这样给小芸讲解的:
,求sin2α的值.小娟是这样给小芸讲解的:
构造如图1所示的图形,在⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°,作CD⊥AB于D.设∠BAC=α,则sinα= ![]() ,可设BC=x,则AB=3x,….
,可设BC=x,则AB=3x,….
(1)【问题解决】
请按照小娟的思路,利用图1求出sin2α的值;(写出完整的解答过程)
(2)如图2,已知点M,N,P为⊙O上的三点,且∠P=β,sinβ= ![]() ,求sin2β的值.
,求sin2β的值.
参考答案:
【答案】
(1)解:如图1中,⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°,作CD⊥AB于D.设∠BAC=α,则sinα= ![]() ,可设BC=x,则AB=3x.
,可设BC=x,则AB=3x.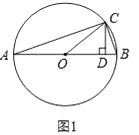
∴AC= ![]() =
= ![]() =2
=2 ![]() x,
x,
∵ ![]() ACBC=
ACBC= ![]() ABCD,
ABCD,
∴CD= ![]() x,
x,
∵OA=OC,
∴∠OAC=∠OCA=α,
∴∠COB=2α,
∴sin2α= ![]() =
= ![]()
(2)解:如图2中,连接NO,并延长交⊙O于点Q,连接MQ,MO,过点M作MR⊥NO于点R.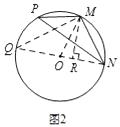
在⊙O中,∠NMQ=90°,
∵∠Q=∠P=β,∴∠MON=2∠Q=2β,
在Rt△QMN中,∵sinβ= ![]() ,
,
∴设MN=3k,则NQ=5k,易得OM= ![]() NQ=
NQ= ![]() ,
,
∴MQ= ![]() =4k,
=4k,
∵ ![]() ,
,
∴3k4k=5kMR
∴MR= ![]() ,
,
在Rt△MRO中,sin2β=sin∠MON= 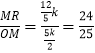 .
.
【解析】(1)通过圆周角定理构造2倍关系角和直角三角形,利用正弦定义可求出sin2α的值;(2)借鉴(1)的方法,通过圆周角定理把圆周角∠P转化为一条边过圆心的圆周角,进而构造出2倍角,利用定义求出正弦.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个角的两边与另一个角的两边分别平行,那么这两个角的大小有什么数量关系?请说明理由。(要求:画出图形,并写出已知,求证,证明过程)。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC, EF∥BC,∠AEF=143°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为多少米?(结果精确到0.1.参考数据:sin 37° ≈ 0.60,cos 37° ≈ 0.80,tan 37° ≈ 0.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.

(1)求证:PA是⊙O的切线;
(2)若AB=4+ ,BC=2
,BC=2  ,求⊙O的半径.
,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点,与y轴交于C点,对称轴与抛物线相交于点M,与x轴相交于点N.点P是线段MN上的一动点,过点P作PE⊥CP交x轴于点E.
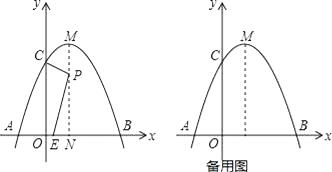
(1)直接写出抛物线的顶点M的坐标是 .
(2)当点E与点O(原点)重合时,求点P的坐标.
(3)点P从M运动到N的过程中,求动点E的运动的路径长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,大正方形的边长为4厘米,小正方形的边长为2厘米,状态如图所示。大正方形固定不动,把小正方形以1厘米∕秒的速度向大正方形的内部沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S厘米2,完成下列问题:

(1)平移到1.5秒时,重叠部分的面积为 厘米2.
(2)求小正方形在平移过程中,S与t的关系式。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=∠ACB。

(1)若D为BC边上一点,E为直线AC上一点,且∠ADE=∠AED.求证:∠BAD=2∠CDE;
(2)如图,若D在BC的反向延长线上,其它条件不变,(1)中的结论是否仍然成立?证明你的结论.

相关试题

