【题目】已知,大正方形的边长为4厘米,小正方形的边长为2厘米,状态如图所示。大正方形固定不动,把小正方形以1厘米∕秒的速度向大正方形的内部沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S厘米2,完成下列问题:

(1)平移到1.5秒时,重叠部分的面积为 厘米2.
(2)求小正方形在平移过程中,S与t的关系式。
参考答案:
【答案】(1)3;(2)当0≤t<2时S=2t;当2≤t≤4时S=4;当4<t≤6时S=12-2t;当6<t时, S=0.;
【解析】
(1)1.5秒时,小正方形向右移动1.5厘米,即可计算出重叠部分面积;
(2)分情况讨论,当0≤t<2时,当2≤t≤4时,当4<t≤6时,当6<t时,分别用t表示出S即可.
解:(1)1.5秒时,小正方形向右移动1.5厘米,S=2×1.5=3cm2,
故答案为:3;
(2)分情况讨论:
①当0≤t<2时,小正方形未完全进入大正方形,此时S=2t,
当2≤t≤4时,小正方形完全在大正方形内,此时S=2×2=4,
当4<t≤6时,小正方形逐渐离开大正方形,此时S=2×2-2×(t-4)=12-2t,
当6<t时,无重叠部分,此时S=0.
综上所述,小正方形在平移过程中,当0≤t<2时S=2t;当2≤t≤4时S=4;当4<t≤6时S=12-2t;当6<t时, S=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.

(1)求证:PA是⊙O的切线;
(2)若AB=4+ ,BC=2
,BC=2  ,求⊙O的半径.
,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】【问题学习】小芸在小组学习时问小娟这样一个问题:已知α为锐角,且sinα=
 ,求sin2α的值.小娟是这样给小芸讲解的:
,求sin2α的值.小娟是这样给小芸讲解的:
构造如图1所示的图形,在⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°,作CD⊥AB于D.设∠BAC=α,则sinα= ,可设BC=x,则AB=3x,….
,可设BC=x,则AB=3x,….
(1)【问题解决】
请按照小娟的思路,利用图1求出sin2α的值;(写出完整的解答过程)
(2)如图2,已知点M,N,P为⊙O上的三点,且∠P=β,sinβ= ,求sin2β的值.
,求sin2β的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点,与y轴交于C点,对称轴与抛物线相交于点M,与x轴相交于点N.点P是线段MN上的一动点,过点P作PE⊥CP交x轴于点E.
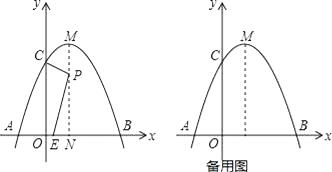
(1)直接写出抛物线的顶点M的坐标是 .
(2)当点E与点O(原点)重合时,求点P的坐标.
(3)点P从M运动到N的过程中,求动点E的运动的路径长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=∠ACB。

(1)若D为BC边上一点,E为直线AC上一点,且∠ADE=∠AED.求证:∠BAD=2∠CDE;
(2)如图,若D在BC的反向延长线上,其它条件不变,(1)中的结论是否仍然成立?证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践
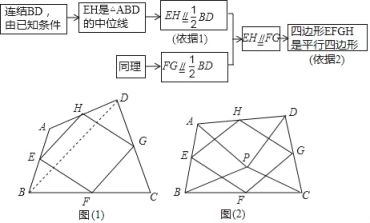
问题情境:在数学活动课上,我们给出如下定义:顺次连按任意一个四边形各边中点所得的四边形叫中点四边形.如图(1),在四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.试说明中点四边形EFGH是平行四边形.
探究展示:勤奋小组的解题思路:
反思交流:
(1)①上述解题思路中的“依据1”、“依据2”分别是什么?
依据1: ;依据2: ;
②连接AC,若AC=BD时,则中点四边形EFGH的形状为 ;
创新小组受到勤奋小组的启发,继续探究:
(2)如图(2),点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并说明理由;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其它条件不变,则中点四边形EFGH的形状为 .
-
科目: 来源: 题型:
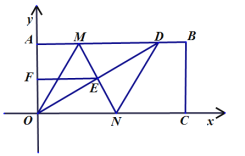
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知矩形AOCB的顶点O、A的坐标分别是(0,0)、(0,a),且满足
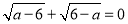 . 点D是AB上一点, M,N垂直平分OD,分别交AB,OD,OC于点M,E,N,连接OM,DN.
. 点D是AB上一点, M,N垂直平分OD,分别交AB,OD,OC于点M,E,N,连接OM,DN.(1)填空:a = ;
(2)求证:四边形MOND是菱形;
(3)若F为OA的中点,连接EF,且满足EF+OE=9,求四边形MOND的周长和面积.
相关试题

