【题目】某超市销售每台进价分别为180元、150元的甲、乙两种型号的电器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
甲种型号 | 乙种型号 | ||
第一周 | 2台 | 3台 | 1100元 |
第二周 | 4台 | 5台 | 2000元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求甲、乙两种型号的电器的销售单价;
(2)若超市准备用不多于5000元的金额再采购这两种型号的电器共30台,求甲种型号的电器最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电器能否实现利润超过1900元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
参考答案:
【答案】(1)A、B两种型号电器的销售单价分别为250元、200元;(2)超市最多采购A种型号电器13台时,采购金额不多于5000元;(3)超市不能实现利润1900元的目标.
【解析】
(1)设甲、乙两种型号电器的销售单价分别为x元、y元,根据2台甲型号3台乙型号的电器收入1100元,4台甲型号5台乙型号的电器收入2000元,列方程组求解;
(2)设采购甲种型号电器a台,则采购乙种型号电器(30-a)台,根据金额不多于5000元,列不等式求解;
(3)设利润为1900元,列方程求出a的值为20,不符合(2)的条件,可知不能实现目标.
(1)设A、B两种型号电器的销售单价分别为x元、y元,
依题意得:![]() ,
,
解得:![]() .
.
答:A、B两种型号电器的销售单价分别为250元、200元;
(2)设采购A种型号电器a台,则采购B种型号电器(30-a)台.
依题意得:180a+150(30-a)≤5000,
解得:a≤![]() .
.
答:超市最多采购A种型号电器13台时,采购金额不多于5000元;
(3)依题意有:(250-180)a+(200-150)(30-a)=1900,
解得:a=20,
∵a≤![]() ,
,
∴在(2)的条件下超市不能实现利润1900元的目标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, 平分
平分 ,
, 平分
平分 ,
, ,
, 相交于点
相交于点 ,
, ,
, .
.
(1)求证:四边形
 是菱形;
是菱形;(2)若
 ,
, ,求
,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次
第二次
第三次
第四次
第五次
第六次
平均成绩
中位数
甲
10
8
9
8
10
9
9
①
乙
10
7
10
10
9
8
②
9.5
(1)完成表中填空① ;② ;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为
 ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
 中,点
中,点 在边
在边 上,
上, ,
, .
.
(1)求证:
 ;
;(2)延长
 至点
至点 ,使
,使 ,连接
,连接 ,
, .判断线段
.判断线段 ,
, 的关系,并证明你的结论.
的关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图(1),如果AB∥CD∥EF. 那么∠BAC+∠ACE+∠CEF=360°.
老师要求学生在完成这道教材上的题目后,尝试对图形进行变式,继续做拓展探究,看看有什么新发现?
(1)小华首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小华用到的平行线性质可能是______________.
(2)接下来,小华用《几何画板》对图形进行了变式,她先画了两条平行线AB,EF,然后在平行线间画了一点C,连接AC,EC后,用鼠标拖动点C,分别得到了图(2)(3)(4),小华发现图(3)正是上面题目的原型,于是她由上题的结论猜想到图(2)和(4)中的∠BAC,∠ACE与∠CEF之间也可能存在着某种数量关系.然后,她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
请你在小华操作探究的基础上,继续完成下面的问题:
①猜想:图(2)中∠BAC,∠ACE与∠CEF之间的数量关系: .
②补全图(4),并直接写出图中∠BAC,∠ACE与∠CEF之间的数量关系: . (3)小华继续探究:如图(5),若直线AB与直线EF不平行,点G,H分别在直线AB、直线EF上,点C在两直线外,连接CG,CH,GH,且GH同时平分∠BGC和∠FHC,请探索∠AGC,∠GCH与∠CHE之间的数量关系?并说明理由.


-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是中国古代数学专著,在数学上有其独到的成就,不仅最早提到了分数问题,也首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱.问买鸡的人数、鸡的价格各是多少?请解答上述问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 、
、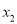 是关于
是关于 的方程
的方程 的两个不相等的实数根.
的两个不相等的实数根.(1)求实数
 的取值范围;
的取值范围;(2)已知等腰
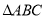 的一边长为7,若
的一边长为7,若 、
、 恰好是
恰好是 另外两边长,求这个三角形的周长.
另外两边长,求这个三角形的周长.
相关试题

