【题目】已知椭圆C: ![]() =1(a>0)的焦点在x轴上,且椭圆C的焦距为2. (Ⅰ)求椭圆C的标准方程;
=1(a>0)的焦点在x轴上,且椭圆C的焦距为2. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)过点R(4,0)的直线l与椭圆C交于两点P,Q,过P作PN⊥x轴且与椭圆C交于另一点N,F为椭圆C的右焦点,求证:三点N,F,Q在同一条直线上.
参考答案:
【答案】解:(Ⅰ)∵椭圆 ![]() 的焦点在x轴上, ∴a2>7﹣a2 , 即
的焦点在x轴上, ∴a2>7﹣a2 , 即 ![]() ,
,
∵椭圆C的焦距为2,且a2﹣b2=c2 ,
∴a2﹣(7﹣a2)=1,解得a2=4,
∴椭圆C的标准方程为 ![]() ;
;
(Ⅱ)证明:由题知直线l的斜率存在,
设l的方程为y=k(x﹣4),点P(x1 , y1),Q(x2 , y2),N(x1 , ﹣y1),
则 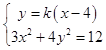 得3x2+4k2(x﹣4)2=12,
得3x2+4k2(x﹣4)2=12,
即(3+4k2)x2﹣32k2x+64k2﹣12=0,△>0, ![]() ,
, ![]() ,
,
由题可得直线QN方程为 ![]() ,
,
又∵y1=k(x1﹣4),y2=k(x2﹣4),
∴直线QN方程为 ![]() ,
,
令y=0,整理得 ![]() =
= ![]()
=  =
= 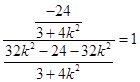 ,
,
即直线QN过点(1,0),
又∵椭圆C的右焦点坐标为F(1,0),
∴三点N,F,Q在同一条直线上.
【解析】(Ⅰ)由椭圆的焦点位置分析可得a2>7﹣a2 , 进而由椭圆的几何性质可得a2﹣(7﹣a2)=1,解可得a的值,代入椭圆的方程即可得答案;(Ⅱ)分析可得直线l的斜率存在,设l的方程为y=k(x﹣4),联立直线与椭圆的方程,由根与系数的关系分析可得直线QN方程,令y=0,可得直线QN过点(1,0),由椭圆的几何性质分析可得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设Sn是数列{an}的前n项和,an>0,且4Sn=an(an+2). (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=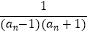 ,Tn=b1+b2+…+bn , 求证:Tn<
,Tn=b1+b2+…+bn , 求证:Tn<  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】医学上某种还没有完全攻克的疾病,治疗时需要通过药物控制其中的两项指标H和V.现有..三种不同配方的药剂,根据分析,A,B,C三种药剂能控制H指标的概率分别为0.5,0.6,0.75,能控制V指标的概率分别是0.6,0.5,0.4,能否控制H指标与能否控制V指标之间相互没有影响. (Ⅰ)求A,B,C三种药剂中恰有一种能控制H指标的概率;
(Ⅱ)某种药剂能使两项指标H和V都得到控制就说该药剂有治疗效果.求三种药剂中有治疗效果的药剂种数X的分布列. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,棱柱ABCD﹣A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,AB=1,AC=
 ,BC=BB1=2.
,BC=BB1=2. 
(Ⅰ)求证:AC⊥平面ABB1A1;
(Ⅱ)求二面角A﹣C1D﹣C的平面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(x2﹣2x)1nx+ax2+2,g(x)=f(x)﹣x﹣2. (Ⅰ)当a=﹣1时,求f(x)在(1,f(1))处的切线方程;
(Ⅱ)若a>0且函数g(x)有且仅有一个零点,求实数a的值;
(Ⅲ)在(Ⅱ)的条件下,若e﹣2<x<e时,g(x)≤m恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xoy中,曲线C的参数方程为
 (t为参数),以O为极点x轴的正半轴为极轴建极坐标系,直线l的极坐标方程为ρ(cosθ﹣sinθ)=4,且与曲线C相交于A,B两点. (Ⅰ)在直角坐标系下求曲线C与直线l的普通方程;
(t为参数),以O为极点x轴的正半轴为极轴建极坐标系,直线l的极坐标方程为ρ(cosθ﹣sinθ)=4,且与曲线C相交于A,B两点. (Ⅰ)在直角坐标系下求曲线C与直线l的普通方程;
(Ⅱ)求△AOB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=m﹣|x﹣1|,(m>0),且f(x+1)≥0的解集为[﹣3,3]. (Ⅰ)求m的值;
(Ⅱ)若正实数a,b,c满足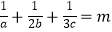 ,求证:a+2b+3c≥3.
,求证:a+2b+3c≥3.
相关试题

