【题目】如图1,在等腰梯形ABCD中,AD//BC,E是AB的中点,过点E作EF//BC交CD于点F,AB=4,BC=6,∠B=60°.
(1)求点E到BC的距离;
(2)点P为线段EF上的一个动点,过点P作PM⊥EF交BC于M,过M作MN//AB交折线ADC于N,连结PN,设EP=x.
①当点N在线段AD上时(如图2),△PMN的形状是否发生改变?若不变,求出△PMN的周长;若改变,请说明理由;
②当点N在线段DC上时(如图3),是否存在点P,使△PMN为等腰三角形?若存在,请求出所有满足条件的x的值;若不存在,请说明理由.



图1 图2 图3
参考答案:
【答案】(1) ![]() (2)
(2) ![]() +
+![]() +4 当x=2或4或5-
+4 当x=2或4或5-![]() 时,△PMN为等腰三角形
时,△PMN为等腰三角形
【解析】【试题分析】(1)在直角三角形BEG中,利用三角函数求解;(2)①如图4,当点N在线段AD上时,△PMN的形状不发生改变.过点N作NH⊥EF于H,设PH与NM交于点Q.先求PQ、PN、PM,再求出MN,最后求出△PMN的周长即可;②按照当PM=PN时, 当MP=MN时,当NP=NM时, 三种情况分类讨论即可.
【试题解析】
(1)如图4,过点E作EG⊥BC于G.
在Rt△BEG中, ![]() ,∠B=60°,
,∠B=60°,
所以![]() ,
, ![]() .
.
所以点E到BC的距离为![]() .
.
(2)因为AD//EF//BC,E是AB的中点,所以F是DC的中点.
因此EF是梯形ABCD的中位线,EF=4.
①如图4,当点N在线段AD上时,△PMN的形状不发生改变.
过点N作NH⊥EF于H,设PH与NM交于点Q.
在矩形EGMP中,EP=GM=x,PM=EG=![]() .
.
在平行四边形BMQE中,BM=EQ=1+x.
所以BG=PQ=1.
因为PM与NH平行且相等,所以PH与NM互相平分,PH=2PQ=2.
在Rt△PNH中,NH=![]() ,PH=2,所以PN=
,PH=2,所以PN=![]() .
.
在平行四边形ABMN中,MN=AB=4.
因此△PMN的周长为![]() +
+![]() +4.
+4.
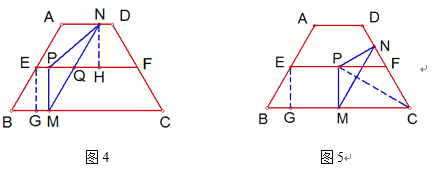
②当点N在线段DC上时,△CMN恒为等边三角形.
如图5,当PM=PN时,△PMC与△PNC关于直线PC对称,点P在∠DCB的平分线上.
在Rt△PCM中,PM=![]() ,∠PCM=30°,所以MC=3.
,∠PCM=30°,所以MC=3.
此时M、P分别为BC、EF的中点,x=2.
如图6,当MP=MN时,MP=MN=MC=![]() ,x=GM=GC-MC=5-
,x=GM=GC-MC=5-![]() .
.
如图7,当NP=NM时,∠NMP=∠NPM=30°,所以∠PNM=120°.
又因为∠FNM=120°,所以P与F重合.
此时x=4.
综上所述,当x=2或4或5-![]() 时,△PMN为等腰三角形.
时,△PMN为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】试根据图中信息,解答下列问题.

(1)一次性购买6根跳绳需_____元,一次性购买12根跳绳需______元;
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
-
科目: 来源: 题型:
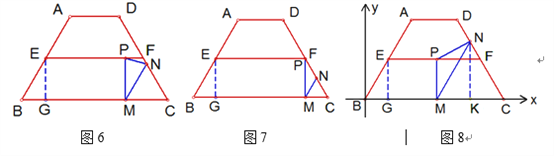
查看答案和解析>>【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括最大值但不包括最小值),请你根据统计图解决下列问题:
(1)此次抽样调查的样本容量是
(2)补全左侧统计图,并求扇形统计图中“25吨~30吨”部分的圆心角度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?

-
科目: 来源: 题型:
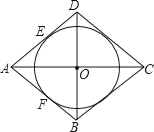
查看答案和解析>>【题目】如图,已知⊙O与等腰△ABD的两腰AB、AD分别相切于点E、F,连接AO并延长到点C,使OC=AO,连接CD、CB.
(1)试判断四边形ABCD的形状,并说明理由;
(2)若AB=4cm,填空:
①当⊙O的半径为 cm时,△ABD为等边三角形;
②当⊙O的半径为 cm时,四边形ABCD为正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】The coordinates of the three points A.B.C on the plane are (﹣5,﹣5),(﹣2,﹣1)and(﹣1,﹣2)respectively,the triangle ABC is( )
(英汉小词典:right直角的;isosceles等腰的;equilateral等边的;obtuse钝角的)
A. a right trisngleB. an isosceles triangle
C. an equilateral triangleD. an obtuse triangle
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A.篮球 B.乒乓球C.羽毛球 D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,

请回答下列问题:
(1)这次被调查的学生共有多少人?
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从①
 ,②
,② ,③
,③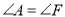 三个条件中选出两个作为已知条件,另一个作为结论可以组成3个命题.
三个条件中选出两个作为已知条件,另一个作为结论可以组成3个命题.
(1)这三个命题中,真命题的个数为________;
(2)选择一个真命题,并且证明.(要求写出每一步的依据)
相关试题

