搜索
【题目】试根据图中信息，解答下列问题.
（1）一次性购买6根跳绳需_____元，一次性购买12根跳绳需______元；
（2）小红比小明多买2根，付款时小红反而比小明少5元，你认为有这种可能吗？若有，请求出小红购买跳绳的根数；若没有，请说明理由.
参考答案：
【答案】(1)150；240；（2）11根.
【解析】
（1）根据单价×数量=总价，求出6根跳绳需多少元；购买12根跳绳，超过10根，打八折是指现价是原价的80%，用单价×数量×0.8即可求出购买12根跳绳需多少元；
（2）有这种可能，可以设小红购买x跳绳根，那么小明购买x-2根跳绳，列出方程25x×0.8=25（x-2）-5，解答即可．
解：（1）一次性购买6根跳绳需25×6=150（元）；
一次性购买12根跳绳需25×12×0.8=240（元）；
故答案为：150；240．
（2）设小红购买x跳绳根，那么小明购买（x-2）根跳绳，
25x×0.8=25（x-2）-5，
解得：x=11；
小明购买了：11-2=9根.
答：小红购买11根跳绳．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，我们把对角线互相垂直的四边形叫做垂美四边形．
(l)概念理解：如图2，在四边形ABCD中，AB=AD，CB=CD，问四边形ABCD是垂美四边形吗？请说明理由．
(2)性质探宄：试探索垂美四边形ABCD两组对边AB，CD与BC，AD之间的数量关系．
猜想结论:（要求用文字语言叙述）
写出证明过程（先画出图形，写出已知、求证）
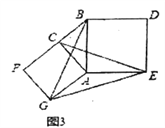
(3)问题解决：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE，已知AC=4，AB=5,求GE长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形AOBC中，O为坐标原点，OA、OB分别在x轴、y轴上，点B的坐标为（0，3
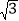），∠ABO=30°，将△ABC沿AB所在直线对折后，点C落在点D处，则点D的坐标为_____．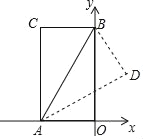
-
科目： 来源： 题型：
查看答案和解析>>【题目】电业部门每月都按时取居民家查电表，电表读数与上次读数的差就是这段时间内用电的千瓦时数．上月初小亮家电表显示的度数为
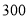，本月初电表显示的读数为
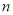．（1）小亮家上月用电多少千瓦时？
（2）如果每千瓦时的电费为
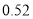元，全月的电费为
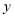（元），那么上月小亮家应缴费电费与本月初电表显示读数之间的关系式是什么？（3）在问题（2）中，哪些量是常量？哪些量是变量？
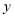是哪个变量的函数？ -
科目： 来源： 题型：
查看答案和解析>>【题目】某市为提倡节约用水，准备实行自来水“阶梯计费”方式，用户用水不超出基本用水量的部分享受基本价格，超出基本用水量的部分实行加价收费，为更好地做决策，自来水公司随机抽取部分用户的用水量数据，并绘制了如图不完整的统计图（每组数据包括最大值但不包括最小值），请你根据统计图解决下列问题：
（1）此次抽样调查的样本容量是
（2）补全左侧统计图，并求扇形统计图中“25吨～30吨”部分的圆心角度数．
（3）如果自来水公司将基本用水量定为每户25吨，那么该地区6万用户中约有多少用户的用水全部享受基本价格？
-
科目： 来源： 题型：
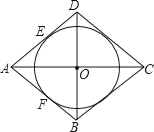
查看答案和解析>>【题目】如图，已知⊙O与等腰△ABD的两腰AB、AD分别相切于点E、F，连接AO并延长到点C，使OC=AO，连接CD、CB．
（1）试判断四边形ABCD的形状，并说明理由；
（2）若AB=4cm，填空：
①当⊙O的半径为 cm时，△ABD为等边三角形；
②当⊙O的半径为 cm时，四边形ABCD为正方形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在等腰梯形ABCD中，AD//BC，E是AB的中点，过点E作EF//BC交CD于点F，AB＝4，BC＝6，∠B＝60°．
（1）求点E到BC的距离；
（2）点P为线段EF上的一个动点，过点P作PM⊥EF交BC于M，过M作MN//AB交折线ADC于N，连结PN，设EP＝x．
①当点N在线段AD上时（如图2），△PMN的形状是否发生改变？若不变，求出△PMN的周长；若改变，请说明理由；
②当点N在线段DC上时（如图3），是否存在点P，使△PMN为等腰三角形？若存在，请求出所有满足条件的x的值；若不存在，请说明理由．
图1 图2 图3
相关试题
