【题目】如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为1个单位,运动时间为t秒.过点P作PE⊥AO交AB于点E.
(1)求直线AB的解析式;
(2)设△PEQ的面积为S,求S与t时间的函数关系,并指出自变量t的取值范围;
(3)在动点P、Q运动的过程中,点H是矩形AOBC内(包括边界)一点,且以B、Q、E、H为顶点的四边形是菱形,直接写出t值和与其对应的点H的坐标.

参考答案:
【答案】(1)直线AB的解析式为y=﹣2x+4.(2)S![]() t2﹣t(2<t≤4).(3)t1=
t2﹣t(2<t≤4).(3)t1=![]() ,H1(
,H1(![]() ),t2=20﹣
),t2=20﹣![]() ,H2(10﹣
,H2(10﹣![]() ,4).
,4).
【解析】试题分析:(1)根据待定系数法即可得到;
(2)过点Q作QF//x轴交y轴于点F,有两种情况:当0<t<2时,PF=4﹣2t,当2<t≤4时,PF=2t﹣4,然后根据面积公式即可求得;
(3)由菱形的邻边相等即可得到.
试题解析:(1)∵C(2,4),
∴A(0,4),B(2,0),
设直线AB的解析式为y=kx+b,
∴![]() ,
,
解得![]()
∴直线AB的解析式为y=﹣2x+4.
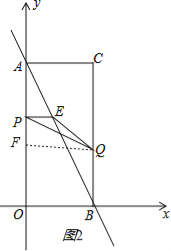
(2)如图2,过点Q作QF⊥y轴于F,
∵PE//OB,
∴![]()
∴有AP=BQ=t,PE=![]() t,AF=CQ=4﹣t,
t,AF=CQ=4﹣t,
当0<t<2时,PF=4﹣2t,
∴S=![]() PEPF=
PEPF=![]() ×
×![]() t(4﹣2t)=t﹣
t(4﹣2t)=t﹣![]() t2,
t2,
即S=﹣![]() t2+t(0<t<2),
t2+t(0<t<2),
当2<t≤4时,PF=2t﹣4,
∴S=![]() PEPF=
PEPF=![]() ×
×![]() t(2t﹣4)=
t(2t﹣4)=![]() t2﹣t(2<t≤4).
t2﹣t(2<t≤4).
(3)t1=![]() ,H1(
,H1(![]() ,
,![]() ),
),
t2=20﹣8![]() ,H2(10﹣4
,H2(10﹣4![]() ,4).
,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】两辆汽车从相距84 km的两地同时出发相向而行,甲车的速度比乙车的速度快20 km/h,半小时后两车相遇.
(1)求乙车的速度是每小时多少千米?
(2)甲车的速度是_______ km/h;
(3)两车相遇时,甲车比乙车多行驶________千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售部有销售人员14人,为提高工作效率和员工的积极性,准备实行“每月定额销售,超额有奖”的措施.调查这14位销售人员某月的销售量,获得数据如下表:
月销售量(件)
145
55
37
30
24
18
人数(人)
1
1
2
5
3
2
(1)求这14位营销人员该月销售量的平均数和中位数
(2)如果你是该公司的销售部管理者,你将如何确定这个定额?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=3x与反比例函数y=
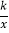 (k≠0)的图象交于A(1,m)和点B.
(k≠0)的图象交于A(1,m)和点B.
(1)求m,k的值,并直接写出点B的坐标;
(2)过点P(t,0)(-1≤t≤1)作x轴的垂线分别交直线y=3x与反比函数y=
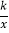 (k≠0)的图象于点E,F.
(k≠0)的图象于点E,F.①当t=
 时,求线段EF的长;
时,求线段EF的长;②若0<EF≤8,请根据图象直接写出t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,F为AD的中点,DE=
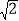 ,CF⊥BD分别交BD,AD于点E,F,连接BF.
,CF⊥BD分别交BD,AD于点E,F,连接BF.(1)求证:EC=2EF;
(2)求四边形BCDF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.
ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF. 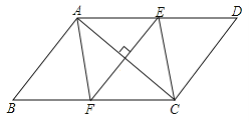
(1)求证:四边形AECF是菱形
(2)若AB=6,BC=10,F为BC中点,求四边形AECF的面积
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)图①表内的各横行中,从第二个数起的数都比它左边相邻的数大m;各竖列中, 从第二个数起的数都比它上边相邻的数大n.请你仔细观察表格,耐心寻找规律, 根据你得到的规律填空:
①m =______;②n =______;③x =______;④y =______;
(2)若(1)题中的规律不变,把表①中的-1,8和y都去掉,如图②,则x=_______(用含m,n的式子表示).

相关试题

