【题目】如图(1),AB∥CD,猜想∠BPD与∠B.∠D的关系,说明理由.(提示:三角形的内角和等于180°)
①填空或填写理由
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°______
∵AB∥CD,EF∥AB,
∴______∥_____,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD+______=180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
②依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B.∠D的关系,并说明理由.

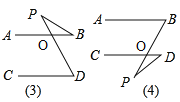
③观察图(3)和(4),已知AB∥CD,直接写出图中的∠BPD与∠B.∠D的关系,不说明理由.
参考答案:
【答案】①
两直线平行,同旁内角互补;CD;EF;∠CDP②猜想∠BPD=∠B+∠D,理由见解析③(3)∠BPD+∠B=∠D;(4)∠BPD=∠B∠D.
【解析】
①过点P作EF∥AB,根据两直线平行,同旁内角互补,证出结论;
②与①的方法类似,过点P作EP∥AB,根据两直线平行,内错角相等,证出结论;
③根据平行线的性质及三角形外角定理即可求解.
①猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB,
∴CD∥EF,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD+∠CDP=180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
故填:两直线平行,同旁内角互补;CD;EF;∠CDP
②猜想∠BPD=∠B+∠D
理由:过点P作EP∥AB,
∴∠B=∠BPE(两直线平行,同位角相等)
∵AB∥CD,EF∥AB,
∴CD∥EF,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD=∠D
∴∠BPD=∠B+∠D

③如图(3),PD、AB交于O点,
∵AB∥CD,∴∠D=∠AOP,
∵∠AOP=∠BPD+∠B,
∴∠BPD+∠B=∠D;
即∠BPD与∠B、∠D的关系为∠BPD+∠B=∠D;
如图(4),PB、CD交于O点,
∵AB∥CD,∴∠B=∠COP,
∵∠COP=∠BPD+∠D,
∴∠BPD+∠D=∠B;
即∠BPD与∠B、∠D的关系为∠BPD=∠B∠D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市举行“行动起来,对抗雾霾”为主题的植树活动,某街道积极响应,决定对该街道进行绿化改造,共购进甲、乙两种树共500棵,已知甲树每棵800元,乙树每棵1200元.
(1)若购买两种树总金额为560000元,求甲、乙两种树各购买了多少棵?
(2)若购买甲树的金额不少于购买乙树的金额,至少应购买甲树多少棵? -
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数y=
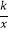 (k≠0)与一次函数y=mx+b(m≠0)交于点A(1,2k﹣1).
(k≠0)与一次函数y=mx+b(m≠0)交于点A(1,2k﹣1).
(1)求反比例函数的解析式;
(2)若一次函数与x轴交于点B,且△AOB的面积为3,求一次函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠C=90°,AD是∠BAC的角分线.

(1)以AB上的一点O为圆心,AD为弦在图中作出⊙O.(不写作法,保留作图痕迹);
(2)试判断直线BC与⊙O的位置关系,并证明你的结论.
(3)若∠B=30°,计算S△DAC:S△ABC的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)36x2-49=0;
(2)(x-3)2=64;
(3)8x3﹣27=0;
(4)4(x﹣1)2﹣121=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系xOy中的位置如图所示.

(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.

(1)求证:△ODM∽△MCN;
(2)设DM=x,求OA的长(用含x的代数式表示);
(3)在点O的运动过程中,设△CMN的周长为P,试用含x的代数式表示P,你能发现怎样的结论?
相关试题

