【题目】反比例函数y= ![]() (k≠0)与一次函数y=mx+b(m≠0)交于点A(1,2k﹣1).
(k≠0)与一次函数y=mx+b(m≠0)交于点A(1,2k﹣1).
(1)求反比例函数的解析式;
(2)若一次函数与x轴交于点B,且△AOB的面积为3,求一次函数的解析式.
参考答案:
【答案】
(1)解:把A(1,2k﹣1)代入y= ![]() 得,
得,
2k﹣1=k,
∴k=1,
∴反比例函数的解析式为:y= ![]()
(2)解:由(1)得k=1,
∴A(1,1),
设B(a,0),
∴S△AOB= ![]() |a|×1=3,
|a|×1=3,
∴a=±6,
∴B(﹣6,0)或(6,0),
把A(1,1),B(﹣6,0)代入y=mx+b得: ![]() ,
,
∴  ,
,
∴一次函数的解析式为:y= ![]() x+
x+ ![]() ,
,
把A(1,1),B(6,0)代入y=mx+b得: ![]() ,
,
∴  ,
,
∴一次函数的解析式为:y=﹣ ![]() .
.
所以符合条件的一次函数解析式为:y=﹣ ![]() 或y=
或y= ![]() x+
x+ ![]()
【解析】(1)利用待定系数法即可求出反比例函数解析式;(2)由S△AOB= ![]() |a|×1=3,求出B的坐标,把A、B坐标代入一次函数解析式 即可求出.
|a|×1=3,求出B的坐标,把A、B坐标代入一次函数解析式 即可求出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空,完成下列证明过程,并在括号中注明理由.
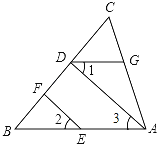
如图,已知∠CGD=∠CAB,∠1=∠2,求证:∠ADF+∠CFE=180°
证明:∵∠CGD=∠CAB
∴DG∥______(______)
∴∠1=______(______)
∵∠1=∠2
∴∠2=∠3(______)
∴EF∥______(______)
∴∠ADF+∠CFE=180°(______)
-
科目: 来源: 题型:
查看答案和解析>>【题目】锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是 .
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是 .
(3)如果锐锐将每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市举行“行动起来,对抗雾霾”为主题的植树活动,某街道积极响应,决定对该街道进行绿化改造,共购进甲、乙两种树共500棵,已知甲树每棵800元,乙树每棵1200元.
(1)若购买两种树总金额为560000元,求甲、乙两种树各购买了多少棵?
(2)若购买甲树的金额不少于购买乙树的金额,至少应购买甲树多少棵? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠C=90°,AD是∠BAC的角分线.

(1)以AB上的一点O为圆心,AD为弦在图中作出⊙O.(不写作法,保留作图痕迹);
(2)试判断直线BC与⊙O的位置关系,并证明你的结论.
(3)若∠B=30°,计算S△DAC:S△ABC的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),AB∥CD,猜想∠BPD与∠B.∠D的关系,说明理由.(提示:三角形的内角和等于180°)
①填空或填写理由
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°______
∵AB∥CD,EF∥AB,
∴______∥_____,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD+______=180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
②依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B.∠D的关系,并说明理由.

③观察图(3)和(4),已知AB∥CD,直接写出图中的∠BPD与∠B.∠D的关系,不说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)36x2-49=0;
(2)(x-3)2=64;
(3)8x3﹣27=0;
(4)4(x﹣1)2﹣121=0.
相关试题

