【题目】如图,在等腰直角三角形MNC中.CN=MN= ![]() ,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O. 
(1)∠NCO的度数为;
(2)求证:△CAM为等边三角形;
(3)连接AN,求线段AN的长.
参考答案:
【答案】
(1)15°
(2)证明:∵∠ACM=60°,CM=CA,
∴△CAM为等边三角形
(3)解:连接AN并延长,交CM于D,
∵△MNC是等腰直角三角形,△ACM是等边三角形,
∴NC=NM= ![]() ,CM=2,AC=AM=2,
,CM=2,AC=AM=2,
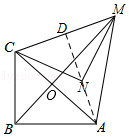
在△ACN和△AMN中,
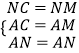 ,
,
∴△ACN≌△AMN(SSS),
∴∠CAN=∠MAN,
∴AD⊥CM,CD= ![]() CM=1,
CM=1,
∴Rt△ACD中,AD= ![]() CD=
CD= ![]() ,
,
等腰Rt△MNC中,DN= ![]() CM=1,
CM=1,
∴AN=AD﹣ND= ![]() ﹣1.
﹣1.
【解析】(1)由旋转可得∠ACM=60°,再根据等腰直角三角形MNC中,∠MCN=45°,运用角的和差关系进行计算即可得到∠NCO的度数;(2)根据有一个角是60°的等腰三角形是等边三角形进行证明即可;(3)根据△MNC是等腰直角三角形,△ACM是等边三角形,判定△ACN≌△AMN,再根据Rt△ACD中,AD= ![]() CD=
CD= ![]() ,等腰Rt△MNC中,DN=
,等腰Rt△MNC中,DN= ![]() CM=1,即可得到AN=AD﹣ND=
CM=1,即可得到AN=AD﹣ND= ![]() ﹣1.
﹣1.
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°,以及对等边三角形的判定的理解,了解三个角都相等的三角形是等边三角形;有一个角等于60°的等腰三角形是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在八次数学测试中,甲、乙两人的成绩如下:
甲:89,93,88,91,94,90,88,87 乙:92,90,85,93,95,86,87,92
请你从下列角度比较两人成绩的情况,并说明理由:
(1)分别计算两人的极差;并说明谁的成绩变化范围大;
(2)根据平均数来判断两人的成绩谁优谁次;
(3)根据众数来判断两人的成绩谁优谁次;
(4)根据中位数来判断两人的成绩谁优谁次;
(5)根据方差来判断两人的成绩谁更稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学五次数学测验成绩如下表:
请你在表中的空白处填上适当的数,用学到的统计知识对两位同学的成绩(单位:分)进行分析,并写出一条合理化建议.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某班通过一次射击测试,在甲、乙两名同学中选出一名同学代表班级参加校射击比赛,这两位同学在相同条件下各射靶5次,所测得的成绩分别如下:(单位:环)

根据测试的成绩,你认为应该由谁代表班级参赛?
-
科目: 来源: 题型:
查看答案和解析>>【题目】菲尔兹奖是国际上有崇高声誉的一个数学奖项,下面的数据是从1936年至2014年菲尔兹奖得主获奖时的年龄(岁): 29 39 35 33 39 27 33 35 31 31 37 32 38 36
31 39 32 38 37 34 29 34 38 32 35 36 33 32
29 35 36 37 39 38 40 38 37 39 38 34 33 40
36 36 37 40 31 38 38 40 40 37 35 40 39 37
请根据上述数据,解答下列问题:
小彬按“组距为5”列出了如图的频数分布表分组
频数
A:25~30
B:30~35
15
C:35~40
31
D:40~45
合计
56
(1)每组数据含最小值不含最大值,请将表中空缺的部分补充完整,并补全频数分布直方图;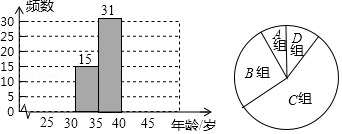
(2)根据(1)中的频数分布直方图描述这56位菲尔兹奖得主获奖时的年龄的分布特征;
(3)在(1)的基础上,小彬又画了如图所示的扇形统计图,图中获奖年龄在30~35岁的人数约占获奖总人数的%(百分号前保留1位小数);C组所在扇形对应的圆心角度数约为°(保留整数) -
科目: 来源: 题型:
查看答案和解析>>【题目】振兴中学某班的学生对本校学生会倡导的“抗震救灾,众志成城”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3∶4∶5∶8∶6,又知此次调查中捐款25元和30元的学生一共42人.

(1)他们一共调查了多少人?
(2)这组数据的众数、中位数各是多少?
(3)若该校共有1560名学生,估计全校学生捐款多少元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 1,∠AOC=∠BOD=90°.
(1)如果∠DOC=28°,那么∠AOB 的度数是多少?
(2)∠AOD ∠BOC(填“>”、“=”或“<”),理由是 .
(3)在图2 中利用能够画直角的工具再画一个与∠COB 相等的角.

相关试题

